Question

The armature of a generator of resistance $1\Omega $ is rotated at its rated speed and produces $125V$ without load and $115V$ with full load. Determine the current in the armature coil.
A) $240A$
B) $10A$
C) $1A$
D) $2A$

Answer 1

Hint: In this question, we will use Kirchhoff’s Voltage law (KVL). It states that in any closed loop network, the total voltage around the loop is equal to the algebraic sum of all the voltage drops within the same loop, which also is equal to zero.

Formula used:
$\sum V = 0$where $\sum V$is the algebraic sum of all voltage drops within the loop.

Complete step by step solution:
Resistance (R) of the armature is $1\Omega $ .
The armature is rotating at its rated speed and produces emf (E) of $125V.$
When the armature rotates with full load, the back emf (Eb) becomes $115V.$
We have to determine the current (i) in the armature coil.
From KVL, we know $\sum V = 0$

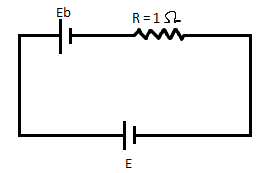
By applying KVL in the loop as shown in the figure, we get $ - E + Eb + (i \times R) = 0$
Now, by rearranging the equation, we get $i = \dfrac{{(E - Eb)}}{R}$
Substituting the given values, $i = \dfrac{{(125 - 115)}}{1} = 10A$

Hence, the current (i) in the armature coil is $10A.$

Additional Information:
In the year 1845, a German physicist named Gustav Kirchhoff developed a pair or set of rules or laws to deal with the conservation of current and energy within electrical circuits. These two rules are commonly known as: Kirchhoff’s Circuit Laws dealing with the current flowing around a closed circuit, and Kirchhoff’s Voltage Law, (KVL) deals with the voltage sources present in a closed circuit.

Note: Whenever these types of questions appear, remember to consider all the voltage drops within the loop. According to KVL, the term ‘algebraic sum’ means to take into account the polarities and signs of the sources and voltage drops within the loop.