Question

The angle of elevation of the summit of a mountain from a point on the ground is \[{45^ \circ }\]. After climbing up one km towards the summit at an inclination of \[{30^ \circ }\] from the ground, the angle of elevation of the summit is found to be \[{60^ \circ }\]. Determine the height of the summit from the ground (in km).
A. \[\dfrac{1}{{\sqrt 3 + 1}}\]
B. \[\dfrac{{\sqrt 3 + 1}}{{\sqrt 3 - 1}}\]
C. \[\dfrac{{\sqrt 3 - 1}}{{\sqrt 3 + 1}}\]
D. \[\dfrac{1}{{\sqrt 3 - 1}}\]

Answer 1

Hint: In this question, we need to find the height of the summit from the ground in km. For this, we will show graphical representation for the above situation. That makes it easier to find the end result. For calculating height, we will use the different trigonometric ratios.

Formula used: The trigonometric ratios in the right angled triangle are given below.
 \[\sin \theta = \dfrac{{{\text{Opposite side}}}}{{Hypotenuse}}\]
\[\cos \theta = \dfrac{{{\text{Adjacent side}}}}{{Hypotenuse}}\]
\[\tan \theta = \dfrac{{{\text{Opposite side}}}}{{{\text{Adjacent side}}}}\]

Complete step-by-step answer:
Consider the following figure that illustrates the given situation.
Here, we need to find h.
Also, AB represents the summit of a mountain.
According to the condition of climbing one km, we can say that the length of CD is 1.

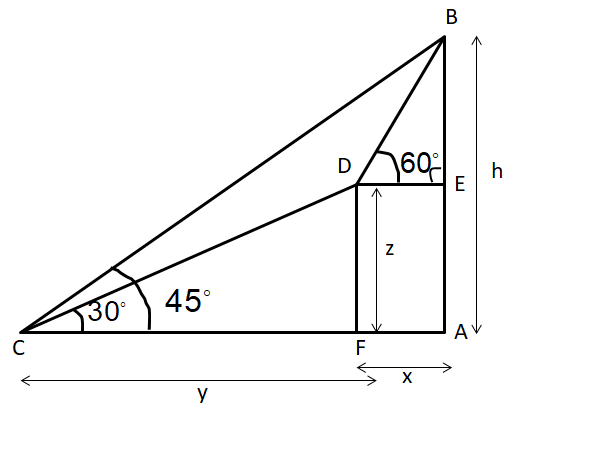
Image: Graphical representation of Given problem
Here, \[CD = 1\]
Also, \[\angle BCA = {45^ \circ },\angle DCA = {30^ \circ },\angle BDE = {60^ \circ }\]
Here, in triangle CDF
\[\sin \theta = \dfrac{{{\text{Opposite side}}}}{{Hypotenuse}}\]
By applying this rule, we get
\[\sin {30^ \circ } = \dfrac{{{\text{DF}}}}{{DC}}\]
\[\sin {30^ \circ } = \dfrac{{\text{z}}}{1}\]
Let us simplify this.
But \[\sin {30^ \circ } = \dfrac{1}{2}\]
Thus, we get
\[\dfrac{1}{2} = \dfrac{{\text{z}}}{1}\]
So, \[z = 1/2\] km
Also, we can say that \[\cos {30^ \circ } = \dfrac{{CF}}{{CD}}\] as \[\cos \theta = \dfrac{{{\text{Adjacent side}}}}{{Hypotenuse}}\]
That means, \[\cos {30^ \circ } = \dfrac{y}{1}\]
But \[\cos {30^ \circ } = \dfrac{{\sqrt 3 }}{2}\]
Thus, we get
\[\dfrac{{\sqrt 3 }}{2} = \dfrac{y}{1}\]
So, \[y = \dfrac{{\sqrt 3 }}{2}\] km
Now, in triangle ABC
\[\tan \theta = \dfrac{{{\text{Opposite side}}}}{{{\text{Adjacent side}}}}\]
By using this rule, we get
\[\tan {45^ \circ } = \dfrac{{AB}}{{AC}}\]
\[\tan {45^ \circ } = \dfrac{h}{{x + y}}\]
But \[\tan {45^ \circ } = 1\]
Thus, we get
\[1 = \dfrac{h}{{x + y}}\]
So, \[h = x + y\] km
But \[\dfrac{{\sqrt 3 }}{2} = y\]
We can find the value of x from the above equation.
So, \[x = h - \dfrac{{\sqrt 3 }}{2}\]
In triangle BDE,
\[\tan \theta = \dfrac{{{\text{Opposite side}}}}{{{\text{Adjacent side}}}}\]
So, we get
\[\tan {60^ \circ } = \dfrac{{h - z}}{x}\]
Now, put \[x = h - \dfrac{{\sqrt 3 }}{2}\] in the above equation.
Thus, we get
\[\tan {60^ \circ } = \dfrac{{h - z}}{{h - \dfrac{{\sqrt 3 }}{2}}}\]
We know that, \[z = 1/2\] km and \[\tan {60^ \circ } = \sqrt 3 \]
So, \[\sqrt 3 = \dfrac{{h - \left( {\dfrac{1}{2}} \right)}}{{\dfrac{{2h - \sqrt 3 }}{2}}}\]
By simplifying, we get
\[\sqrt 3 = \dfrac{{2h - 1}}{2} \times \dfrac{2}{{2h - \sqrt 3 }}\]
\[\sqrt 3 = \dfrac{{2h - 1}}{{2h - \sqrt 3 }}\]
\[2h\sqrt 3 - 3 = 2h - 1\]
By simplifying further, we get
\[2h\sqrt 3 - 2h = 3 - 1\]
\[2h\left( {\sqrt 3 - 1} \right) = 2\]
\[h\left( {\sqrt 3 - 1} \right) = 1\]
\[h = \dfrac{1}{{\left( {\sqrt 3 - 1} \right)}}\]
As a result, the summit's height from the ground is \[\dfrac{1}{{\left( {\sqrt 3 - 1} \right)}}\] km.
Therefore, the correct option is (D).

Note: Many students make mistakes in presenting the given situation graphically. Also, they may get confused in the simplification part for finding the height. For solving this question, we should know how to apply trigonometric ratios in the right-angled triangle and their values for the angles such as \[{30^ \circ },{45^ \circ },{60^ \circ }\]etc.