Question

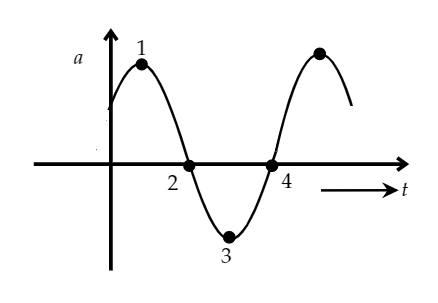
The acceleration of a particle undergoing S.H.M is shown in the figure. Which of the labelled points corresponds to the particle being at \[ - {x_{\max }}\]?

A. 4
B. 3
C. 2
D. 1

Answer 1

Hint: Here, we need to recall the term SHM. A simple harmonic motion is a good example of periodic motion. In simple harmonic motion, a particle will be accelerated towards a fixed point and the acceleration of the particle is proportional to the magnitude of the displacement of the particle. A good example of simple harmonic motion is the oscillation of a mass suspended at the end of spring.

Formula Used:
The formula acceleration in SHM is,
\[a = - {\omega ^2}x\]
Where, x is distance of a wave and \[\omega \] is angular velocity of a wave.

Complete step by step solution:

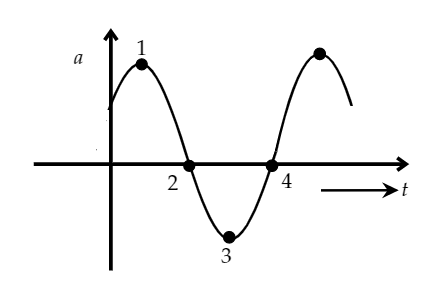
Image: Acceleration of a particle undergoing S.H.M

Consider a particle that is undergoing S.H.M at some acceleration as shown in the figure. We need to find which of the labelled points corresponds to the particle being at negative x-axis.
As we know that the acceleration in SHM is,
\[a = - {\omega ^2}x\]
At \[x = - {x_{\max }}\]
Acceleration will be,
\[\therefore a = + {\omega ^2}{x_{\max }}\]
As we can see from the figure, the acceleration will be maximum and positive. Therefore, at point 1, ‘a’ will be maximum and positive.

Hence, option D is the correct answer.

Note: Here, in this given problem we have seen that the displacement of the particle executing SHM will be dependent on amplitude, angular frequency, and time. We have to remember the formula for the velocity and acceleration of the given particle using its displacement. That is why both the quantities depend on the same parameters.