Question

Seven homogeneous bricks each of length L, mass M are arranged as shown. Projection $x = \dfrac{L}{{10}}$ then x coordinate of center of mass is:

Answer 1

- Hint: In order to solve this question, firstly we will assume that the bricks are placed on one another and length, mass be L, m respectively. Then we will apply the formula of center of mass i.e. ${X_{cm}} = \dfrac{{{M_1}{X_1} + {M_2}{X_2} + {M_3}{X_3}.....}}{{{M_1} + {M_2} + {M_3}.......}}$ to get the required answer.

Formula used-
${X_{cm}} = \dfrac{{{M_1}{X_1} + {M_2}{X_2} + {M_3}{X_3}.....}}{{{M_1} + {M_2} + {M_3}.......}}$

Complete step-by-step solution -

The center of mass is a point in a system that responds to outside forces as if at this point the total mass of the system was concentrated. The center of mass can be determined by taking the masses from which you seek to locate the center of mass, and by multiplying them by their locations. You then add these together, and divide it by the sum of all the masses.
Let mass of brick be M and length be L.
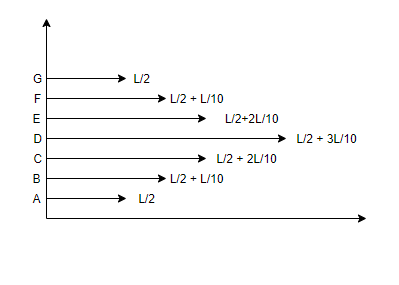
Assuming that each brick is in contact by distance $x = \dfrac{L}{{10}}$. In addition, the bricks are put on each other and the first and last bricks have the same center of mass, the second and sixth having the same center of mass, the third and fifth having the same center of mass, the fourth having a different center of mass.
Let the bricks be called A, B , C, D, E, F, G
$ \Rightarrow Com{\text{ of A,G = }}\dfrac{L}{2}$
$ \Rightarrow Com{\text{ of B,F = }}\dfrac{L}{2} + \dfrac{L}{{10}}$
$ \Rightarrow Com{\text{ of C, E = }}\dfrac{L}{2} + \dfrac{{2L}}{{10}}$
$ \Rightarrow Com{\text{ of D = }}\dfrac{L}{2} + \dfrac{{3L}}{{10}}$
Using the formula of center of mass i.e.${X_{cm}} = \dfrac{{{M_1}{X_1} + {M_2}{X_2} + {M_3}{X_3}.....}}{{{M_1} + {M_2} + {M_3}.......}}$
Now, center of mass of X coordinate is-
$X = \dfrac{{\left( {{M_1}{X_1} + {M_2}{X_2} + {M_3}{X_3} + {M_4}{X_4} + {M_5}{X_5} + {M_6}{X_6} + {M_7}{X_7}} \right)}}{{{M_1} + {M_2} + {M_3} + {M_4} + {M_5} + {M_6} + {M_7}}}$
$X = \dfrac{{\left\{ {2 \times \dfrac{{ML}}{2} + 2 \times M\left( {\dfrac{L}{2} + \dfrac{L}{{10}}} \right) + 2 \times M\left( {\dfrac{L}{2} + \dfrac{{2L}}{{10}}} \right) + M \times \left( {\dfrac{L}{2} + \dfrac{{3L}}{{10}}} \right)} \right\}}}{{7M}}$
$X = \dfrac{{\left[ {ML + 2M\left\{ {\dfrac{{\left( {5L + L} \right)}}{{10}}} \right\} + 2M\left\{ {\dfrac{{\left( {5L + 2L} \right)}}{{10}}} \right\} + M \times \left\{ {\dfrac{{\left( {5L + 3L} \right)}}{{10}}} \right\}} \right]}}{{7M}}$
$X = \dfrac{{\left( {10ML + 12ML + 14ML + 8ML} \right)}}{{10 \times 7M}}$
$\Rightarrow X = \dfrac{{44ML}}{{70M}}$
$\Rightarrow X = \dfrac{{44L}}{{70}}$
$\Rightarrow X = \dfrac{{22L}}{{35}}$
Therefore, we conclude that the X coordinate of center of mass, $X = \dfrac{{22L}}{{35}}$.

Note- While solving this question, we must know the concept of center of mass i.e. it is a position defined relative to an object or system of objects. It is the average location of all components of the system, weighted by their masses.