Question

A trolly falling freely on an inclined plane as shown in the figure. The angle of string of pendulum with the ceiling of trolley is $\left( \alpha \right)$ equal to-


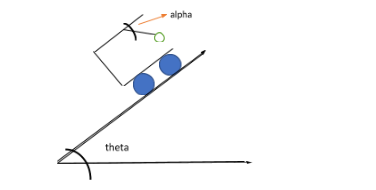
(A). ${\theta ^ \circ }$
(B). ${90^ \circ } - {\theta ^ \circ }$
(C). ${90^ \circ }$
(D). ${0^ \circ }$

Answer 1

- Hint: We will add the component of tension and component of weight and put it in the formula of force in order to solve this question. The formula for force is $F = ma$.

Complete step-by-step solution -

Let T be the tension acting on the trolley.
So, the component of tension along the inclined plane is $T\cos \alpha $.
If m is the mass of the system of trolley, then the component of weight along the inclined plane is $mg\sin \theta $.
As we know that the acceleration of the trolley is equal to the acceleration of the bob in the trolley as bob is in the equilibrium in the frame of the trolley.
So, the net force along the plane will be-
$
   \Rightarrow F = ma \\
    \\
   \Rightarrow mg\sin \theta + T\cos \alpha = ma \\
$
For the free falling trolly on an inclined plane, acceleration $a = g\sin \theta $ along the plane.
So, putting this value of acceleration in the above formula, we get-
$
   \Rightarrow mg\sin \theta + T\cos \alpha = ma \\
    \\
   \Rightarrow mg\sin \theta + T\cos \alpha = mg\sin \theta \\
$
Cancelling $mg\sin \theta $ from both the sides, we get-
$
   \Rightarrow mg\sin \theta + T\cos \alpha = mg\sin \theta \\
    \\
   \Rightarrow T\cos \alpha = 0 \\
    \\
   \Rightarrow \cos \alpha = 0 \\
    \\
   \Rightarrow \alpha = {90^ \circ } \\
$
Hence, option C is the correct option.

Note: In physics, tension is depicted as the pulling force transmitted axially by the methods for a string, a cable, chain, or comparative one-dimensional continuous object, or by each finish of a bar, truss member, or comparable three-dimensional object; tension may likewise be portrayed as the action-reaction pair of forces acting at each finish of said elements.