Question

Select the correct mirror image for the word SHARE.

A) A
B) B
C) C
D) D

Answer 1

Hint: A mirror creates virtual and erect. However, the image is inverted in the left-right direction. The human eye lens creates a real inverted image of this virtual image on the retina.

Complete step by step solution:
The human eye’s working is pure ray optics. The light enters the eye through the pupil and falls off the eye lens, then the eye lens converges those light rays into one point on the retina to form a real inverted image of the object.
In the image of an object formed by the eye lens, the nature of this image is real and inverted. But when we see an image formed by a plane mirror, the image is a virtual image and it is erect but the orientation of this image is different from the object, it is inverted in the left-right direction. So, in order to find the mirror image of the word share along a mirror in the right side we need to turn everything by 180 degrees in the horizontal (left-right) direction.
The steps for finding the correct image are:
Step1: write the entire word in reverse order.
Step2: rotate each alphabet 180 degrees in the left-right direction.
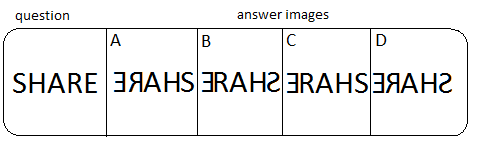
For option A:

Here, first the entire word is written in reverse order.
Then we have to check one by one if all alphabets are rotated or not:
Let’s start with E then all the way to S:
E is rotated.
R is rotated.
A is symmetrical so rotated A looks the same as A, so yes, A is rotated.
H is symmetrical so rotated H looks the same as H, so yes, H is rotated.
S is not rotated.
Hence, option A is not correct.

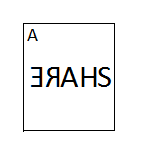
For option B:

Here, the word is written in reverse order.
Let’s start with E all the way to S to check if all the alphabets are rotated or not?
E is rotated.
R is not rotated.
Hence, Option B is not the answer.

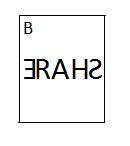
For option C:

Here, the entire word is written in reverse order.
Let’s start with E all the way to S to check if all alphabets are rotated or not.
E is rotated.
R is not rotated.
Hence, option C is not the answer.

For option D:

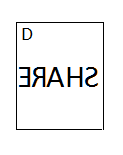
Here, the entire word is written in reversed order.
Let’s start with E all the way to S to check if all alphabets are rotated or no?
E is rotated.
R is rotated.
A is rotated.
H is rotated.
S is rotated.
All alphabets are rotated by 180 degrees in the left-right direction. Thus, this is the mirror image of the word ‘SHARE’.

Hence, the answer is D.

Note: Images formed by a plane mirror are virtual, erect and of the same size. Treating them as normal objects in cases like the above would help do the problem quickly. Considering magnification of an image in the case of a plane mirror will only confuse you as magnification in case of plane mirror is 1.