Pulley mass system is shown in figure string and pulleys and strings are ideal. Acceleration of $m_{2}$ and $m_{1}$ will be:

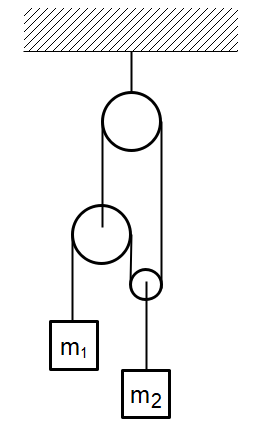
A) $a_{1} = 2 a_{2}$
B) $a_{1} = 2 a_{1}$
C) $a_{1} = a_{2} = g$
D) $a_{1} = 3 a_{2}$

Answer

Verified

148.8k+ views

Hint: In this solution, we will draw the free body diagram of the string pulley system. Then we will calculate the tension in the strings to calculate the acceleration in the two blocks.

Complete step by step answer:
Let us start by drawing a free body diagram of the tension in the different strings.

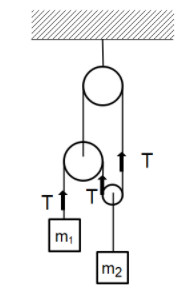
AS we can see, for the mass

m_{1}

the mass it experiences is associated with only the bottom left pulley. Hence, we can write the equation of motion for the first mass as:

T = m a_{1}

Now the string connecting the lower two pulleys is the same so the net displacement will be zero. Also, we can see that for the pulley in the bottom right, the tension in the two strings will be

2 T

as can be seen from the diagram. Also, the tension in the string can be represented as the acceleration of the object which will be

T = 2 m a_{2}

Since the tension will be the same in the string for both the bottom pulleys, we have

m a_{1} = 2 m a_{2}

So, the relation of the acceleration of the two blocks will be

a_{1} = 2 a_{2}

Hence the correct choice will be choice (A).

Note: We can intuitively expect the first mass to have higher acceleration since it will have to compensate for the tension exerted by the other mass as it is connected by two pulleys. As a result, the displacement of the first block will always be higher than the displacement of the second block. We shouldn’t worry about the movement of individual pulleys but only the tension in the strings as it simplifies our calculations.