Question

Maximum value of \[z = 12x + 3y\], subject to constraints \[x \geqslant 0\], \[y \geqslant 0\], \[x + y \leqslant 5\] and \[3x + y \leqslant 9\] is
A. \[15\]
B. \[36\]
C. \[60\]
D. \[40\]

Answer 1

Hint: In this question, create the given lines on graph paper and remember that the optimal value is located on the graph's corner to find the value of the target function at the graph's corners to determine the target function's maxima.

Complete step-by-step solution:
We are given that \[z = 12x + 3y\] subject to constraints
\[
  x \geqslant 0, \\
  y \geqslant 0, \\
  x + y \leqslant 5\,\,\,and \\
  3x + y \leqslant 9
 \]
Now we plot \[x + y \leqslant 5\,\] on the graph:
When \[x = 0\] we have
\[
  x + y = 5 \\
  0 + y = 5 \\
  y = 5
 \]
When \[y = 0\] we have
\[
  x + y = 5 \\
  x + 0 = 5 \\
  x = 5
 \]
Therefore, two points on the line are \[\left( {0,5} \right)\left( {5,0} \right)\]
To check the feasible region we will consider origin and substitute in the inequality. If it holds true then the region which contains origin will be feasible region and if it doesn’t hold true then the region which doesn’t contains origin will be feasible region.
 \[x + y \leqslant 5\,\]
 \[0 + 0 \leqslant 5\,\]
So inequality holds true.
Now by plot these points on the graph, we get

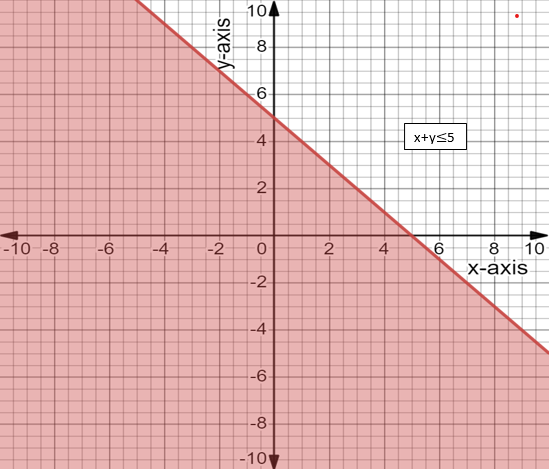
Image: Graph of linear inequality \[x + y \leqslant 5\,\]
Now we plot \[3x + y \leqslant 9\] on the graph:
When \[x = 0\] we have
\[
  3x + y = 9 \\
  3\left( 0 \right) + y = 9 \\
  y = 9 \\
 \]
When \[y = 0\] we have
\[
  3x + 0 = 9 \\
  3x = 9 \\
  x = \dfrac{9}{3} \\
  x = 3 \\
 \]
Therefore, two points on the line are \[\left( {0,9} \right)\left( {3,0} \right)\]
To check the feasible region we will consider origin and substitute in the inequality. If it holds true then the region which contains origin will be the feasible region and if it doesn’t hold true then the region which doesn’t contain origin will be the feasible region.
 \[3x + y \leqslant 9\,\]
 \[0 + 0 \leqslant 9\,\]
So inequality holds true.
Now by plot these points on the graph, we get

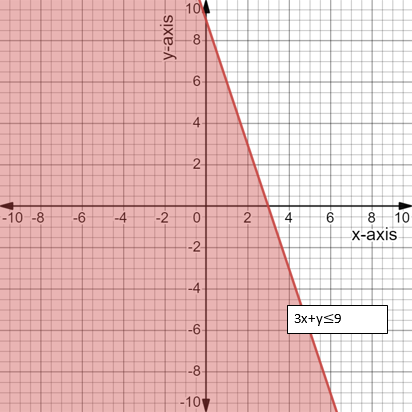
Image: Graph of linear inequality \[3x + y \leqslant 9\,\]
Also, we have \[x \geqslant 0,y \geqslant 0\]

Image: Graph of linear inequalities \[3x + y \leqslant 9\,\] and \[x + y \leqslant 5\,\]
Now we find the value of x and y:
We have two given equations
\[
  x + y \leqslant 5 \\
  3x + y \leqslant 9 \\
 \]
Now we can write these equation as:
\[
  x + y = 5...\left( 1 \right) \\
  3x + y = 9...\left( 2 \right) \\
 \]
Now by subtracting equation (1) from equation (2), we get
\[
  3x + y - x - y = 9 - 5 \\
  2x = 4 \\
  x = \dfrac{4}{2} \\
  x = 2 \\
 \]
Now we substitute the value of x in equation (1), we get
\[
  2 + y = 5 \\
  y = 5 - 2 \\
  y = 3 \\
 \]
Thus the value of x and y is:
\[
  x = 2 \\
  y = 3
 \]
Now we know that the maxima are the maximum value of a function within the given set of ranges. We will check on all the corner points of the feasible region.
At (0, 0), the value of Z = 0.
At (0, 5), the value of Z = 15.
At (3, 0), the value of Z = 36.
And at (2, 3), the value of z,
\[
  z = 12x + 3y \\
   = 12\left( 2 \right) + 3\left( 3 \right) \\
   = 24 + 9 \\
   = 33
 \]
Therefore, the maximum value is 36.
Hence, option (B) is correct answer

Note: It is critical for the solution of a linear programming problem to keep the constraints variables non-negative. The simplex method can also be used to find the maxima of the above problem. The simplex method is an algorithmic process for solving linear programming problems.