




Key Properties and Equations of Straight Lines and Circles
Straight lines and circles are fundamental geometric constructs in coordinate geometry and complex number geometry, forming the basis for various advanced results and exam-level problem solving.
Coordinate and Complex Forms of the Straight Line
Definition: A straight line in the coordinate plane is the locus of points satisfying a linear equation, typically written as $ax + by + c = 0$, where $a$, $b$, $c$ are real constants and $(a, b) \neq (0, 0)$.
The primary forms of the straight line in the Cartesian plane include:
- Point–Slope form
- Two–Point form
- Slope–Intercept form
- Intercept form
- Normal form
Given a fixed point $A(x_1, y_1)$ and slope $m$, the point–slope form is $y - y_1 = m(x - x_1)$.
For points $A(x_1, y_1)$ and $B(x_2, y_2)$, the two–point form is $y-y_1 = \dfrac{y_2-y_1}{x_2-x_1}(x-x_1)$, valid if $x_1 \neq x_2$.
The slope–intercept form, for slope $m$ and $y$-intercept $c$, is $y = mx + c$.
The intercept form, for intercepts $a$ (on $x$-axis) and $b$ (on $y$-axis), is $\dfrac{x}{a} + \dfrac{y}{b} = 1$, provided $a, b \ne 0$.
Equations of Straight Lines in the Complex Plane
Let $z = x + iy$ represent a variable point and $z_0 = x_0 + i y_0$ be fixed. The general equation $ax + by + c = 0$ can be rewritten in complex notation. Recalling $x = \dfrac{z + \overline{z}}{2}$ and $y = \dfrac{z - \overline{z}}{2i}$, substituting yields the complex form:
$a \frac{z + \overline{z}}{2} + b \frac{z - \overline{z}}{2i} + c = 0$
Multiplying both sides by 2, and simplifying using $i^2 = -1$, gives:
$(a - ib)z + (a + ib)\overline{z} + 2c = 0$
Result: The general straight line in the complex plane has the form $\alpha z + \overline{\alpha}\,\overline{z} + k = 0$, where $\alpha$ is complex and $k$ real, $\alpha \ne 0$.
The slope in the complex representation is $-\dfrac{\overline{\alpha}}{\alpha}$.
Parametric Representation and Line Segment Division
The straight line through $z_1$ and $z_2$ in the complex plane is parametrically $z = (1-t)z_1 + t z_2$, where $t \in \mathbb{R}$. Every point on the line can be generated as $t$ varies, and the point dividing the segment $z_1 z_2$ in the ratio $m:n$ is $z = \frac{m z_2 + n z_1}{m + n}$.
For the locus equidistant from two points $p$, $q$ in the complex plane, $\lvert z - p \rvert = \lvert z - q \rvert$ gives the perpendicular bisector of the segment $pq$.
Conditions for Parallelism and Perpendicularity of Lines
Let $w_1$ and $w_2$ denote the slopes of two lines. Result: The lines are parallel if $w_1 = w_2$, and perpendicular if $w_1 w_2 = -1$ in the Cartesian plane. In the complex plane, associate slopes $w_1 = \dfrac{z_1 - z_2}{\overline{z_1} - \overline{z_2}}$ and $w_2 = \dfrac{z_3 - z_4}{\overline{z_3} - \overline{z_4}}$.
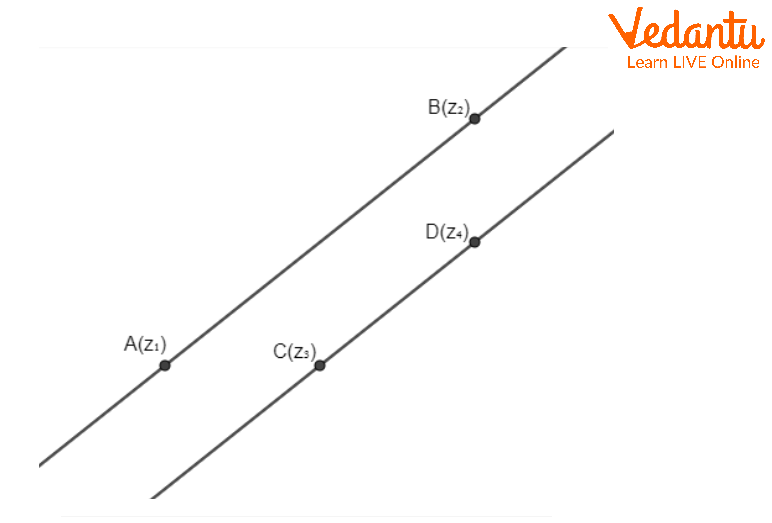
Parallelism: $w_1 = w_2$. For perpendicularity: $w_1 + w_2 = 0$. The arguments of the segments confirm these conditions, with $\operatorname{Arg}\left(\frac{z_1 - z_2}{z_3 - z_4}\right) = 0,\pi$ for parallel and $\pm \frac{\pi}{2}$ for perpendicular cases.
A misconception is to equate the complex slopes directly with real number slopes without considering the chosen orientation in the complex plane.
General Equations of the Circle in Cartesian and Complex Planes
A circle on the Cartesian plane with centre $(h, k)$ and radius $r$ has equation $(x-h)^2 + (y-k)^2 = r^2$.
The general form is $x^2 + y^2 + 2g x + 2f y + c = 0$, with centre $(-g, -f)$ and radius $\sqrt{g^2 + f^2 - c}$, provided $g^2 + f^2 - c > 0$.
Given endpoints $(a,b), (c,d)$ of a diameter, the equation is $(x-a)(x-c) + (y-b)(y-d) = 0$.
In the complex plane, for centre $z_0$ and radius $r$, the locus $\lvert z - z_0 \rvert = r$ forms the circle. Expanding, $\lvert z - z_0 \rvert^2 = (z - z_0)(\overline{z} - \overline{z_0}) = r^2$, which gives the general quadratic form in $z$ and $\overline{z}$.
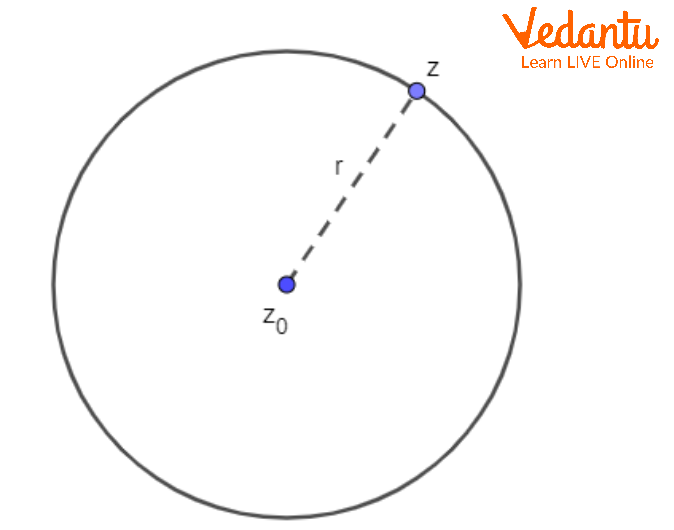
Identity: The general circle through complex geometry is $z\overline{z} + \overline{\alpha}\,z + \alpha\,\overline{z} + k = 0$, with centre $-\alpha$ and radius $\sqrt{|\alpha|^2 - k}$ when $|\alpha|^2 - k > 0$.
Typical JEE Patterns on Straight Lines and Circles
Standard question types include finding intersection points, tangent and normal equations, loci derived from construction or transformation, and recognition of geometric relationships such as concurrency, orthogonality, and collinearity. Problems also frequently test conversion between the complex and Cartesian representations under exam constraints.
Properties And Solutions Of Triangles
Worked Examples Involving Core Results
Example: Find the equation of the line passing through $(1,2)$ with slope $-3$.
Substitute into point–slope form: $y-2 = -3(x-1)$.
Rearrange: $y = -3x + 5$.
Example: Determine the centre and radius of $x^2 + y^2 - 4x + 6y - 12 = 0$.
Rewrite: $x^2-4x + y^2+6y = 12$.
Complete the squares: $(x-2)^2 + (y+3)^2 = 25$.
Centre: $(2,-3)$, radius: $5$.
Example: Express the equation $3x - 2y + 7 = 0$ as a line in the complex plane.
$a = 3, b = -2$, so $\alpha = 3 + 2i$, $k = 7$. The complex line equation is $(3 - 2i)z + (3 + 2i)\overline{z} + 14 = 0$.
Example: For which values of $c$ does $x^2 + y^2 + c = 0$ represent a real circle?
Radius squared is $-c$. Hence, $-c > 0 \implies c < 0$.
Graphs Of Sine And Cosine Function
Interpretation of the Circle and Line in Problem Contexts
When a locus is constrained by equal distances, the resulting equation is of the form $\lvert z - p \rvert = \lvert z - q \rvert$, the perpendicular bisector. When a fixed distance from a point is specified, the locus forms a circle.
A frequent error is omitting the check for the trivial case $g^2 + f^2 - c > 0$ for the existence of a real circle in $x^2 + y^2 + 2gx + 2fy + c = 0$.
FAQs on Understanding Straight Lines and Circles in Geometry
1. What is the equation of a straight line?
The equation of a straight line in its general form is expressed as Ax + By + C = 0. This equation represents all the points (x, y) lying on the line.
Key forms of the equation include:
- Slope-intercept form: y = mx + c, where m is the slope and c is the y-intercept.
- Point-slope form: y - y1 = m(x - x1), where (x1, y1) is a point on the line.
- Intercept form: x/a + y/b = 1, where a and b are the x and y-intercepts respectively.
2. What is the equation of a circle?
The equation of a circle with centre at (h, k) and radius r is (x - h)2 + (y - k)2 = r2.
Key points:
- For a circle centred at the origin, the equation simplifies to x2 + y2 = r2.
- The general form is x2 + y2 + 2gx + 2fy + c = 0, where centre is (-g, -f) and radius is √(g2 + f2 - c).
3. How do you find the point of intersection between a straight line and a circle?
To find the point of intersection between a straight line and a circle, substitute the line's equation into the circle's equation and solve for x and y.
Steps:
- Write the equations:
- Line: y = mx + c
- Circle: (x - h)2 + (y - k)2 = r2
- Substitute y from the line into the circle's equation.
- Solve the resulting quadratic to get x values.
- Find corresponding y values using the line equation.
4. What is the condition for a line to be tangent to a circle?
A line is tangent to a circle if it touches the circle at exactly one point. The condition is:
- The distance from the centre of the circle to the line equals the radius.
- For circle (x - h)2 + (y - k)2 = r2 and line Ax + By + C = 0:
5. How do you find the equation of a circle passing through three given points?
To find the equation of a circle passing through three points (x1,y1), (x2,y2), and (x3,y3), substitute these points into the general circle equation x2 + y2 + 2gx + 2fy + c = 0.
Procedure:
- Write three equations by plugging the points into the general equation.
- Solve the system to find g, f, and c.
- Write the final equation with these values.
6. What does it mean when the discriminant is zero for the intersection of a line and a circle?
A zero discriminant in the quadratic equation obtained when solving for the intersection indicates the line is tangent to the circle.
Key implications:
- Only one solution (point of contact).
- Distance from circle's centre to line equals the radius.
- Relevant in exams for identifying tangency conditions.
7. What is the centre and radius of the circle x2 + y2 + 4x – 6y + 9 = 0?
For x2 + y2 + 4x – 6y + 9 = 0:
- Centre: (-2, 3)
- Radius: 2
Obtained by writing the equation as (x + 2)2 + (y – 3)2 = 4.
8. What is the length of the tangent from a point outside a circle?
The length of the tangent from a point (x1, y1) to the circle (x - h)2 + (y - k)2 = r2 is:
- √[(x1 – h)2 + (y1 – k)2 – r2]
9. How do you write the equation of the tangent to a circle at a given point?
The equation of the tangent to the circle (x – h)2 + (y – k)2 = r2 at the point (x1, y1) is:
- (x1 – h)(x – h) + (y1 – k)(y – k) = r2
10. What is the condition for two circles to touch each other externally?
Two circles touch externally if the distance between their centres equals the sum of their radii.
Condition:
- If centres are (h1, k1) and (h2, k2) with radii r1 and r2:
- √[(h1 – h2)2 + (k1 – k2)2] = r1 + r2
























