




Key Differences Between Signum, Constant, Identity, and Polynomial Functions
Relations and functions describe assignments between sets, with specific types such as signum, constant, identity, and polynomial functions each exhibiting distinct algebraic properties essential for problem solving in advanced mathematics.
Definition and Mathematical Notation for Types of Real-Valued Functions
Definition: A function $f: \mathbb{R} \to \mathbb{R}$ is an assignment associating each real number $x$ to a unique real number $f(x)$. Notable types include signum, constant, identity, and polynomial functions.
The signum function is denoted $\operatorname{sgn}(x)$ and defined by the rule: \[ \operatorname{sgn}(x) = \begin{cases} 1 & \text{if } x > 0 \\ 0 & \text{if } x = 0 \\ -1 & \text{if } x < 0 \end{cases} \]
A constant function is defined as $f(x) = c$ for all $x \in \mathbb{R}$, where $c$ is constant.
An identity function is $f(x) = x$ for all $x \in \mathbb{R}$.
A polynomial function is $f(x) = a_n x^n + \cdots + a_1 x + a_0$ with $a_i \in \mathbb{R}$ and $n \in \mathbb{N} \cup \{0\}$.
Properties and Algebraic Structure of the Signum Function
The signum function is an odd function, satisfying $f(-x) = -f(x)$ for all $x \in \mathbb{R}$.
The algebraic identity $\operatorname{sgn}(x) = \dfrac{x}{|x|}$ holds for all $x \neq 0$ and connects signum with the modulus function.
For $x=0$, $\operatorname{sgn}(0) = 0$ is defined by convention. Its graph has jumps at $x=0$, reflecting a discontinuity.

Domain and Range Analysis for Signum, Constant, Identity, and Polynomial Functions
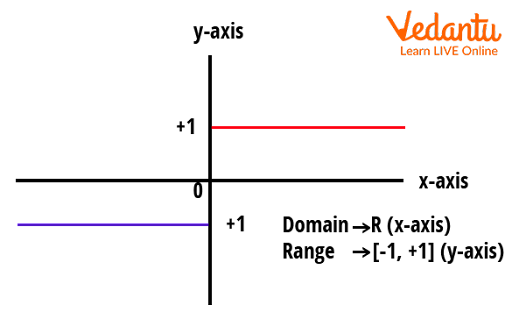
The domain of $\operatorname{sgn}(x)$, constant, identity, and polynomial functions is $\mathbb{R}$, the set of all real numbers.
The range of $\operatorname{sgn}(x)$ is $\{-1, 0, 1\}$. The range of $f(x)=c$ is $\{c\}$. For $f(x)=x$, the range is $\mathbb{R}$. For polynomials, the range depends on degree and coefficients.
For detailed relationships among these function types, consult Relations And Functions Overview.
Algebraic Distinctions between Constant, Identity, and Polynomial Functions
A constant function is polynomial of degree $0$. An identity function is polynomial of degree $1$ with leading coefficient $1$, and no constant term.
Result: Every constant and identity function is a polynomial function, but not every polynomial function is constant or identity.
Polynomial functions may exhibit bounded or unbounded ranges based on degree and leading coefficient parity.
Further structure for related families is found in Functions And Its Types.
Graphical Interpretation and Behaviour of Signum and Related Functions
The graph of $\operatorname{sgn}(x)$ consists of three segments: $y=1$ for $x>0$, $y=0$ at $x=0$, and $y=-1$ for $x<0$.
The graph of $f(x)=c$ is a horizontal line $y=c$. The identity function $f(x)=x$ yields a straight line passing through the origin at $45^\circ$.
A polynomial function graph depends on its degree and leading coefficient, with known behaviour at infinity and turning points.
Domain, range, and symmetry properties are given in Algebra Of Functions.
Continuity and Differentiability of the Signum, Constant, Identity, and Polynomial Functions
All polynomial, constant, and identity functions are continuous and differentiable everywhere on $\mathbb{R}$.
The signum function is continuous for $x \ne 0$ with jump discontinuity at $x=0$, since \[ \lim_{x \to 0^-} \operatorname{sgn}(x) = -1 \neq \lim_{x \to 0^+} \operatorname{sgn}(x) = 1. \] It is not differentiable at $x=0$ due to the discontinuity.
For systematic function properties, examine Sets Relations And Functions.
Illustrative Problems on Evaluation and Application
Example 1: Evaluate $\operatorname{sgn}(-5)$.
Given $x = -5$. Since $x < 0$, substitute to obtain $\operatorname{sgn}(-5) = -1$.
Example 2: Compute $f(3)$ for $f(x) = 7$ (constant function).
Given $x=3$. Substituting yields $f(3)=7$.
Example 3: For $g(x) = x$, find $g(-2.1)$.
Given $x=-2.1$. Thus, $g(-2.1) = -2.1$.
Example 4: If $p(x) = 2x^2 - 3x + 1$, calculate $p(-1)$.
Given $x=-1$. \[ p(-1) = 2(-1)^2 - 3(-1) + 1 = 2(1) + 3 + 1 = 6 \]
Example 5: Find all real solutions to $\operatorname{sgn}(x-2) = 0$.
$\operatorname{sgn}(x-2) = 0$ only when $x-2=0$, so $x=2$.
Key Conceptual Differences and Common Misconceptions
| Aspect | Signum / Constant / Identity / Polynomial |
|---|---|
| Symmetry | Signum: odd; Constant: even; Identity: odd; Polynomial: varies |
| Continuity at $x=0$ | Signum: no; Others: yes |
| Differentiability | Signum: not at $x=0$; Others: everywhere |
| Range (Real) | Signum: $\{-1,0,1\}$; Constant: $\{c\}$; Identity: $\mathbb{R}$; Polynomial: varies |
| Degree | Constant: $0$; Identity: $1$; Polynomial: $n$; Signum: not polynomial |
| Slope | Identity: $1$; Constant: $0$; Signum: undefined at $0$ |
For confusion reduction between function types, see Difference Between Relations And Functions.
- Graph shape and segmentation
- Domain specification
- Range characterization
- Continuity and jump discontinuities
- Algebraic degree
- Symmetry
- Use in function composition
FAQs on Understanding Signum, Constant, Identity, and Polynomial Functions
1. What is a signum function in mathematics?
Signum function (often denoted as sgn(x)) is a special mathematical function that indicates the sign of a real number.
Key points about signum function:
- sgn(x) = 1 for x > 0
- sgn(x) = 0 for x = 0
- sgn(x) = -1 for x < 0
2. What is a constant function? Give an example.
A constant function is a function that always returns the same value regardless of the input.
Key features:
- General form: f(x) = c, where c is a constant
- The graph is a straight line parallel to the x-axis
- Example: f(x) = 5 for all x ∈ ℝ
3. What is the identity function? Explain with its graph.
The identity function is a function where every input maps to itself.
Main points:
- General form: f(x) = x
- Its graph is a straight line passing through the origin with a slope of 1
- It is one of the simplest polynomial functions and plays a key role in understanding other types of functions
4. What is a polynomial function? State its general form.
A polynomial function is a function that can be expressed in the form f(x) = a_n x^n + a_{n-1} x^{n-1} + ... + a_0, where n is a non-negative integer.
Key details:
- Each term includes a coefficient and a variable raised to a non-negative integer power
- Examples include quadratic, cubic, and linear functions
- Polynomial functions are part of the class 11 syllabus under the chapter Relations and Functions
5. What are the main types of functions discussed in the chapter Relations and Functions?
Functions covered in this chapter include:
- Constant Function
- Identity Function
- Signum Function
- Polynomial Function
6. How is the graph of a signum function represented?
The signum function graph consists of three parts:
- A horizontal segment at y = 1 for x > 0
- A single point at (0, 0)
- A horizontal segment at y = -1 for x < 0
7. What distinguishes the identity function from the constant function?
Identity function maps every element to itself, while a constant function maps every element to the same value.
Key differences:
- Identity: f(x) = x
- Constant: f(x) = c (where c is a fixed constant)
8. What are some examples of polynomial functions?
Polynomial function examples include:
- Linear: f(x) = 2x + 1
- Quadratic: f(x) = x² - 4x + 4
- Cubic: f(x) = x³ - 3x + 2
9. Explain the domain and range of the signum function.
The domain of the signum function is all real numbers (ℝ), while its range is {-1, 0, 1}.
Summary:
- Domain: all real numbers
- Range: three distinct values: -1, 0, and 1
10. What are the key differences between relation and function?
A relation shows a connection between any two elements of two sets, while a function is a specific type of relation where every input has exactly one output.
Key points:
- Every function is a relation, but not all relations are functions
- Functions adhere to the rule of unique output for each input
























