
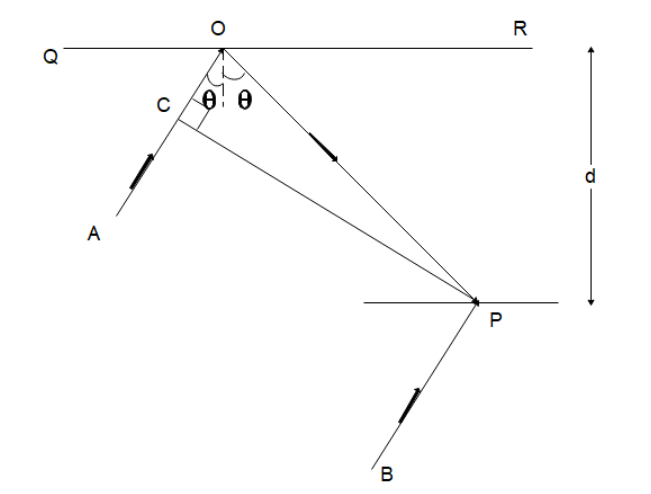
ln the adjacent diagram, CP represents a wavefront and AO and BP, the corresponding two rays. The condition on $\theta $ for constructive interference at P between the ray BP and reflected ray OP is:
A) $\cos \theta = \dfrac{{3\lambda }}{{2d}}$
B) $\cos \theta = \dfrac{\lambda }{{4d}}$
C) $\sec \theta - \cos \theta = \dfrac{\lambda }{d}$
D) $\sec \theta - \cos \theta = \dfrac{{4\lambda }}{d}$
Answer
232.8k+ views
Hint: In this solution, we will first calculate the extra distance by the ray AO before it reaches the point P which will be the path difference of the two rays. There will be constructive interference if the path difference is an integral multiple of the wavelength of the two waves. However, in this case, the reflection of one of the rays from the top surface will flip the condition for constructive interference.
Complete step by step answer:
From the diagram, we can see that while the two rays AO and BP are parallel to each other the ray AO will have to travel an extra distance before it reaches the point P. We know that this is the path difference between the two rays. Let us find the extra distance the ray AO has to travel.
Since the line CP represents a wavefront, the extra distance, the ray AO will travel will be the sum of distance CO and OP.
We can find the distance BP from triangle OPM as:
$\cos \theta = \dfrac{d}{{OP}}$
$ \Rightarrow OP = \dfrac{d}{{\cos \theta }}$
For CO, we can see that
\[\cos 2\theta = \dfrac{{CO}}{{OP}}\]
As $OP = \dfrac{d}{{\cos \theta }}$, we can write
\[ \Rightarrow CO = \dfrac{{d\cos 2\theta }}{{\cos \theta }}\]
Now the net path difference will be
$D = CO + OP$
$ \Rightarrow D = \dfrac{d}{{\cos \theta }}(\cos 2\theta + 1)$
Since \[\cos (2\theta + 1) = 2{\cos ^2}\theta \], we have
$D = 2d\cos \theta $
Under normal circumstances, the path difference would have to be equal to an integral multiple of wavelengths. But in this case, the reflection of the ray OP causes an additional path difference of $\lambda /2$. Hence the condition of the constructive interference, in this case, will be
$\Rightarrow$ $D = \dfrac{{n\lambda }}{2}$ which we can write as
$\Rightarrow$ $2d\cos \theta = \dfrac{{n\lambda }}{2}$
Which gives us
$\cos \theta = \dfrac{{n\lambda }}{{4d}}$
For $n = 1$,
$\cos \theta = \dfrac{\lambda }{{4d}}$ which corresponds to option (B).
Note: We must be careful to include the reflection of the ray OP and its effect on an additional path difference in the ray. For this, we have assumed that the medium outside OQ is rarer than the medium where the waves are propagating.
Complete step by step answer:
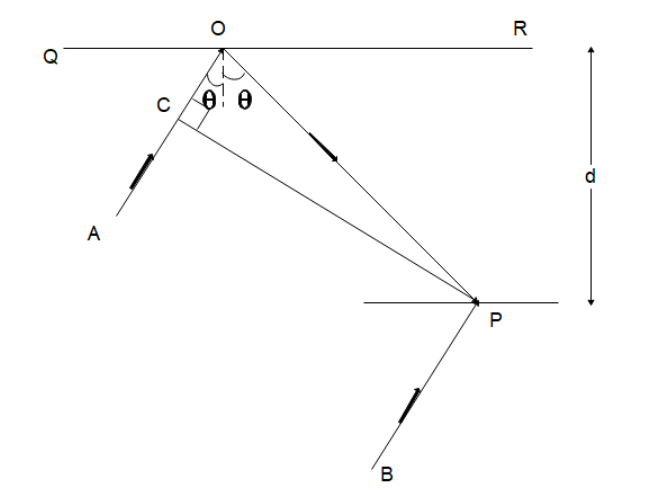
From the diagram, we can see that while the two rays AO and BP are parallel to each other the ray AO will have to travel an extra distance before it reaches the point P. We know that this is the path difference between the two rays. Let us find the extra distance the ray AO has to travel.

Since the line CP represents a wavefront, the extra distance, the ray AO will travel will be the sum of distance CO and OP.
We can find the distance BP from triangle OPM as:
$\cos \theta = \dfrac{d}{{OP}}$
$ \Rightarrow OP = \dfrac{d}{{\cos \theta }}$
For CO, we can see that
\[\cos 2\theta = \dfrac{{CO}}{{OP}}\]
As $OP = \dfrac{d}{{\cos \theta }}$, we can write
\[ \Rightarrow CO = \dfrac{{d\cos 2\theta }}{{\cos \theta }}\]
Now the net path difference will be
$D = CO + OP$
$ \Rightarrow D = \dfrac{d}{{\cos \theta }}(\cos 2\theta + 1)$
Since \[\cos (2\theta + 1) = 2{\cos ^2}\theta \], we have
$D = 2d\cos \theta $
Under normal circumstances, the path difference would have to be equal to an integral multiple of wavelengths. But in this case, the reflection of the ray OP causes an additional path difference of $\lambda /2$. Hence the condition of the constructive interference, in this case, will be
$\Rightarrow$ $D = \dfrac{{n\lambda }}{2}$ which we can write as
$\Rightarrow$ $2d\cos \theta = \dfrac{{n\lambda }}{2}$
Which gives us
$\cos \theta = \dfrac{{n\lambda }}{{4d}}$
For $n = 1$,
$\cos \theta = \dfrac{\lambda }{{4d}}$ which corresponds to option (B).
Note: We must be careful to include the reflection of the ray OP and its effect on an additional path difference in the ray. For this, we have assumed that the medium outside OQ is rarer than the medium where the waves are propagating.
Recently Updated Pages
Dimensions of Charge: Dimensional Formula, Derivation, SI Units & Examples

How to Calculate Moment of Inertia: Step-by-Step Guide & Formulas

Circuit Switching vs Packet Switching: Key Differences Explained

Dimensions of Pressure in Physics: Formula, Derivation & SI Unit

JEE General Topics in Chemistry Important Concepts and Tips

JEE Extractive Metallurgy Important Concepts and Tips for Exam Preparation

Trending doubts
JEE Main 2026: Session 2 Registration Open, City Intimation Slip, Exam Dates, Syllabus & Eligibility

JEE Main 2026 Application Login: Direct Link, Registration, Form Fill, and Steps

JEE Main Marking Scheme 2026- Paper-Wise Marks Distribution and Negative Marking Details

Understanding the Angle of Deviation in a Prism

Hybridisation in Chemistry – Concept, Types & Applications

How to Convert a Galvanometer into an Ammeter or Voltmeter

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Laws of Motion Class 11 Physics Chapter 4 CBSE Notes - 2025-26

Waves Class 11 Physics Chapter 14 CBSE Notes - 2025-26

Mechanical Properties of Fluids Class 11 Physics Chapter 9 CBSE Notes - 2025-26

Thermodynamics Class 11 Physics Chapter 11 CBSE Notes - 2025-26

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26




