
Let C be the circle with centre at (1, 1) and radius 1. If T is the circle centred at (0, k) passing through the origin and touching the circle C externally, then the radius of T is equal to
(1) \[\sqrt {\frac{3}{2}} \]
(2) \[\frac{{\sqrt 3 }}{2}\]
(3) \[\frac{1}{2}\]
(4) \[\frac{1}{4}\]
Answer
217.2k+ views
Hint: In this question, the distance between the center of the two circles whose coordinates are (1,1) and (0,k) respectively will be (1 + k). Apply the formula of the distance between the two points to find the distance between the points.
Formula Used: 1) \[\begin{array}{*{20}{c}}
R& = &{\sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}} }
\end{array}\]
Complete step by step Solution:
According to the given question, the figure is drawn. This figure will give some information about the radius of circle T.
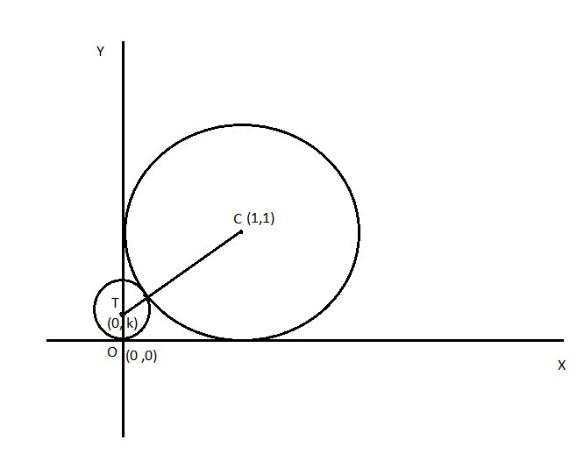
According to the drawn figure, we will get to know that K is the radius of the circle T and the radius of the circle C is 1.
From the figure,
\[\begin{array}{*{20}{c}}
{ \Rightarrow CT}& = &{k + 1}
\end{array}\] …………… (A)
And we know that if there are two points which is at \[R\] distance to each other, then the distance between the coordinates will be written as,
\[\begin{array}{*{20}{c}}
{ \Rightarrow R}& = &{\sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}} }
\end{array}\] ………….. (1)
And the coordinates of the points are given that is C(1, 1) and T(0, k)
Now,
\[\begin{array}{*{20}{c}}
{ \Rightarrow {x_1}}& = &1
\end{array}\] and \[\begin{array}{*{20}{c}}
{{y_1}}& = &1
\end{array}\]
\[\begin{array}{*{20}{c}}
{ \Rightarrow {x_2}}& = &0
\end{array}\] and \[\begin{array}{*{20}{c}}
{{y_2}}& = &k
\end{array}\]
Put these values in equation (1). Therefore, we can write.
\[\begin{array}{*{20}{c}}
{ \Rightarrow R}& = &{\sqrt {{{(0 - 1)}^2} + {{(k - 1)}^2}} }
\end{array}\]
\[\begin{array}{*{20}{c}}
{ \Rightarrow R}& = &{\sqrt {1 + {{(k - 1)}^2}} }
\end{array}\]
\[\begin{array}{*{20}{c}}
{ \Rightarrow R}& = &{\sqrt {{k^2} - 2k + 2} }
\end{array}\]
Now from the figure \[\begin{array}{*{20}{c}}
R& = &{CT}
\end{array}\]. So we can write,
\[\begin{array}{*{20}{c}}
{ \Rightarrow CT}& = &{\sqrt {{k^2} - 2k + 2} }
\end{array}\]………………………… (B)
On comparing the equation (A) and equation (B), we will get.
\[\begin{array}{*{20}{c}}
{ \Rightarrow k + 1}& = &{\sqrt {{k^2} - 2k + 2} }
\end{array}\]
Square both sides in the above equation, we will get.
\[\begin{array}{*{20}{c}}
{ \Rightarrow {{(k + 1)}^2}}& = &{(\sqrt {{k^2} - 2k + 2} }
\end{array}{)^2}\]
Therefore,
\[\begin{array}{*{20}{c}}
{ \Rightarrow {k^2} + 1 + 2k}& = &{{k^2} - 2k + 2}
\end{array}\]
\[\begin{array}{*{20}{c}}
{ \Rightarrow 4k}& = &1
\end{array}\]
\[\begin{array}{*{20}{c}}
{ \Rightarrow k}& = &{\frac{1}{4}}
\end{array}\]
Now the final answer is \[\begin{array}{*{20}{c}}
k& = &{\frac{1}{4}}
\end{array}\]. Therefore,
Hence, the correct option is 4.
Note: The distance between the center of the two circles will be computed with the help of the distance formula of the two coordinates.
Formula Used: 1) \[\begin{array}{*{20}{c}}
R& = &{\sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}} }
\end{array}\]
Complete step by step Solution:
According to the given question, the figure is drawn. This figure will give some information about the radius of circle T.

According to the drawn figure, we will get to know that K is the radius of the circle T and the radius of the circle C is 1.
From the figure,
\[\begin{array}{*{20}{c}}
{ \Rightarrow CT}& = &{k + 1}
\end{array}\] …………… (A)
And we know that if there are two points which is at \[R\] distance to each other, then the distance between the coordinates will be written as,
\[\begin{array}{*{20}{c}}
{ \Rightarrow R}& = &{\sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}} }
\end{array}\] ………….. (1)
And the coordinates of the points are given that is C(1, 1) and T(0, k)
Now,
\[\begin{array}{*{20}{c}}
{ \Rightarrow {x_1}}& = &1
\end{array}\] and \[\begin{array}{*{20}{c}}
{{y_1}}& = &1
\end{array}\]
\[\begin{array}{*{20}{c}}
{ \Rightarrow {x_2}}& = &0
\end{array}\] and \[\begin{array}{*{20}{c}}
{{y_2}}& = &k
\end{array}\]
Put these values in equation (1). Therefore, we can write.
\[\begin{array}{*{20}{c}}
{ \Rightarrow R}& = &{\sqrt {{{(0 - 1)}^2} + {{(k - 1)}^2}} }
\end{array}\]
\[\begin{array}{*{20}{c}}
{ \Rightarrow R}& = &{\sqrt {1 + {{(k - 1)}^2}} }
\end{array}\]
\[\begin{array}{*{20}{c}}
{ \Rightarrow R}& = &{\sqrt {{k^2} - 2k + 2} }
\end{array}\]
Now from the figure \[\begin{array}{*{20}{c}}
R& = &{CT}
\end{array}\]. So we can write,
\[\begin{array}{*{20}{c}}
{ \Rightarrow CT}& = &{\sqrt {{k^2} - 2k + 2} }
\end{array}\]………………………… (B)
On comparing the equation (A) and equation (B), we will get.
\[\begin{array}{*{20}{c}}
{ \Rightarrow k + 1}& = &{\sqrt {{k^2} - 2k + 2} }
\end{array}\]
Square both sides in the above equation, we will get.
\[\begin{array}{*{20}{c}}
{ \Rightarrow {{(k + 1)}^2}}& = &{(\sqrt {{k^2} - 2k + 2} }
\end{array}{)^2}\]
Therefore,
\[\begin{array}{*{20}{c}}
{ \Rightarrow {k^2} + 1 + 2k}& = &{{k^2} - 2k + 2}
\end{array}\]
\[\begin{array}{*{20}{c}}
{ \Rightarrow 4k}& = &1
\end{array}\]
\[\begin{array}{*{20}{c}}
{ \Rightarrow k}& = &{\frac{1}{4}}
\end{array}\]
Now the final answer is \[\begin{array}{*{20}{c}}
k& = &{\frac{1}{4}}
\end{array}\]. Therefore,
Hence, the correct option is 4.
Note: The distance between the center of the two circles will be computed with the help of the distance formula of the two coordinates.
Recently Updated Pages
Area vs Volume: Key Differences Explained for Students

Mutually Exclusive vs Independent Events: Key Differences Explained

Addition of Three Vectors: Methods & Examples

Addition of Vectors: Simple Guide for Students

Algebra Made Easy: Step-by-Step Guide for Students

Relations and Functions: Complete Guide for Students

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

Understanding Collisions: Types and Examples for Students

How to Convert a Galvanometer into an Ammeter or Voltmeter

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

NCERT Solutions for Class 11 Maths Chapter 10 Conic Sections

NCERT Solutions for Class 11 Maths Chapter 9 Straight Lines

NCERT Solutions For Class 11 Maths Chapter 8 Sequences And Series

Understanding Atomic Structure for Beginners

NCERT Solutions For Class 11 Maths Chapter 12 Limits And Derivatives




