




Vector Addition Rules and Easy Solved Examples for Students
The addition of three vectors involves combining their magnitudes and directions according to the axioms of vector addition. This process is essential in advanced vector algebra and underpins the analysis of physical quantities such as force, velocity, and displacement. The addition may be performed using geometric or analytical methods, subject to the representation of the vectors involved.
Addition of Three Vectors Using Analytical Methods
Let $\vec{A}$, $\vec{B}$, and $\vec{C}$ be three vectors in three-dimensional space. The resultant vector, denoted as $\vec{R}$, is defined by the equation \[ \vec{R} = \vec{A} + \vec{B} + \vec{C} \] where addition is performed component-wise.
Express $\vec{A}$, $\vec{B}$, and $\vec{C}$ with respect to the standard basis vectors: \[ \vec{A} = A_x \hat{i} + A_y \hat{j} + A_z \hat{k} \] \[ \vec{B} = B_x \hat{i} + B_y \hat{j} + B_z \hat{k} \] \[ \vec{C} = C_x \hat{i} + C_y \hat{j} + C_z \hat{k} \] where $A_x, A_y, A_z$, etc., denote the respective components along the $x$-, $y$-, and $z$-axes.
The sum of the three vectors is then calculated component-wise: \[ \vec{R} = (A_x+B_x+C_x) \hat{i} + (A_y+B_y+C_y) \hat{j} + (A_z+B_z+C_z) \hat{k} \]
Denoting the resultant components as $R_x = A_x+B_x+C_x$, $R_y = A_y+B_y+C_y$, $R_z = A_z+B_z+C_z$, the magnitude of the resultant vector is given by \[ |\vec{R}| = \sqrt{R_x^2 + R_y^2 + R_z^2} \]
For the case that vectors lie in a plane (planar vectors), the $z$-components vanish, and the resultant is simply \[ |\vec{R}| = \sqrt{R_x^2 + R_y^2} \]
Addition of Three Vectors by Successive Geometric Laws
If magnitudes and the angles between the vectors are specified, but not their components, the resultant is determined through iterative application of the triangle law of vector addition. For two arbitrary vectors $\vec{P}$ and $\vec{Q}$ separated by an angle $\theta$, the triangle law states: \[ |\vec{P}+\vec{Q}| = \sqrt{P^2 + Q^2 + 2PQ \cos\theta} \] where $P = |\vec{P}|$, $Q = |\vec{Q}|$, and $\theta$ is the angle from $\vec{P}$ to $\vec{Q}$.
To add three vectors $\vec{A},\ \vec{B},\ \vec{C}$ represented by magnitudes and angles:
First, find $\vec{R}_1=\vec{A}+\vec{B}$. If the angle between $\vec{A}$ and $\vec{B}$ is $\theta_1$, \[ |\vec{R}_1| = \sqrt{A^2 + B^2 + 2AB\cos\theta_1} \]
Denote $\alpha$ as the angle between $\vec{R}_1$ and $\vec{C}$. The final resultant is computed as \[ |\vec{R}| = \sqrt{|\vec{R}_1|^2 + C^2 + 2|\vec{R}_1|C\cos\alpha} \]
Application of this law requires explicit knowledge of the angles between each step’s resultant and the next vector; geometric construction aids in determining these where not given. For a graphical depiction, refer to the triangle and parallelogram addition laws as detailed in Addition Of Vectors.
Graphical Illustration of Three Vector Addition
The addition of three vectors graphically involves placing the tail of each subsequent vector at the head of the previous one. The resultant $\vec{R}$ is drawn from the tail of the first vector to the head of the last vector. The graphical technique enables visualization of the resultant’s magnitude and direction. Refer to the illustration below:
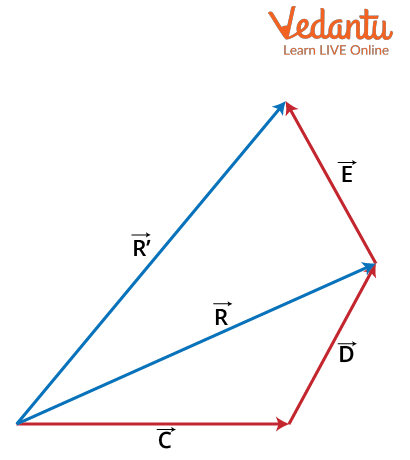
Detailed Derivation: Magnitude of the Resultant When Three Directions and Angles Are Known
Let three vectors $\vec{A},\ \vec{B},\ \vec{C}$ be such that the angle between $\vec{A}$ and $\vec{B}$ is $\theta_1$, and the angle between $\vec{R}_1 = \vec{A}+\vec{B}$ and $\vec{C}$ is $\theta_2$. To determine the magnitude of the resultant step by step:
First, find $|\vec{R}_1|$: \[ |\vec{R}_1| = \sqrt{A^2 + B^2 + 2AB \cos\theta_1} \]
Next, compute $|\vec{R}|$ where $\vec{R} = \vec{R}_1 + \vec{C}$, and $\theta_2$ is the angle between $\vec{R}_1$ and $\vec{C}$. \[ |\vec{R}| = \sqrt{|\vec{R}_1|^2 + C^2 + 2|\vec{R}_1|C\cos\theta_2} \]
Every intermediate calculation must be performed completely and explicitly in practical problems. For details on parallelogram and triangle laws, see Vector Algebra.
Stepwise Example: Component Method for Three Vectors
Given: $\vec{A} = 3\hat{i} + 2\hat{j} + 6\hat{k}$, $\vec{B} = 5\hat{i} - 3\hat{j} + 4\hat{k}$, $\vec{C} = -1\hat{i} + 7\hat{j} - 2\hat{k}$
Resultant: \[ \vec{R} = (3 + 5 + (-1))\hat{i} + (2 + (-3) + 7)\hat{j} + (6 + 4 + (-2))\hat{k} \]
Calculate each component: \[ \begin{align*} R_x &= 3 + 5 + (-1) = 7 \\ R_y &= 2 + (-3) + 7 = 6 \\ R_z &= 6 + 4 + (-2) = 8 \\ \end{align*} \] So, \[ \vec{R} = 7\hat{i} + 6\hat{j} + 8\hat{k} \]
Magnitude: \[ |\vec{R}| = \sqrt{(7)^2 + (6)^2 + (8)^2} \] \[ |\vec{R}| = \sqrt{49 + 36 + 64} \] \[ |\vec{R}| = \sqrt{149} \] \[ |\vec{R}| = 12.206\ (\text{to three decimal places}) \]
For further vector manipulation techniques, see Scalar Product Of Vectors.
Stepwise Example: Magnitude by Successive Triangle Law
Given: $|\vec{A}|=4$ units, $|\vec{B}|=5$ units, $|\vec{C}|=7$ units. The angle between $\vec{A},\vec{B}$ is $90^\circ$, angle between their resultant $\vec{R}_1$ and $\vec{C}$ is $60^\circ$.
First, apply triangle law to $\vec{A}$ and $\vec{B}$: \[ |\vec{R}_1| = \sqrt{4^2 + 5^2 + 2 \times 4 \times 5 \times \cos 90^\circ} \] Since $\cos 90^\circ = 0$, \[ |\vec{R}_1| = \sqrt{16 + 25} \] \[ |\vec{R}_1| = \sqrt{41} \] \[ |\vec{R}_1| = 6.403\ \text{units} \ (\text{rounded to three decimal places}) \]
Now, add $\vec{R}_1$ and $\vec{C}$ with an angle $60^\circ$ between them: \[ |\vec{R}| = \sqrt{(\sqrt{41})^2 + 7^2 + 2 \times \sqrt{41} \times 7 \times \cos 60^\circ} \] Since $\cos 60^\circ = \frac{1}{2}$, \[ |\vec{R}| = \sqrt{41 + 49 + 2 \times \sqrt{41} \times 7 \times \frac{1}{2}} \] \[ |\vec{R}| = \sqrt{41 + 49 + 7\sqrt{41}} \] \[ |\vec{R}| = \sqrt{90 + 7\sqrt{41}} \] \[ 7\sqrt{41} \approx 7 \times 6.403 = 44.821 \] \[ 90 + 44.821 = 134.821 \] \[ |\vec{R}| = \sqrt{134.821} \] \[ |\vec{R}| = 11.614\ \text{units} \ (\text{rounded to three decimal places}) \]
For advanced study on triple and cross products, refer to Vector Triple Product.
Criteria for Zero Sum of Three Vectors
Three vectors $\vec{A}, \vec{B}, \vec{C}$ sum to zero if and only if $\vec{A} + \vec{B} + \vec{C} = \vec{0}$, which implies that the vectors form the consecutive sides of a closed triangle taken in the same order. Analytically, for vectors $\vec{A},\vec{B},\vec{C}$ to satisfy this, \[ \vec{A} + \vec{B} = -\vec{C} \] The geometric interpretation is that placement of the vectors head-to-tail results in a return to the starting point.
Connections to the geometric interpretation of vectors can be found in Geometry Of Complex Numbers.
Associativity and Commutativity in Three Vector Addition
Vector addition is both associative and commutative: \[ \vec{A} + (\vec{B} + \vec{C}) = (\vec{A} + \vec{B}) + \vec{C} \] \[ \vec{A} + \vec{B} + \vec{C} = \vec{C} + \vec{B} + \vec{A} \] These properties allow the sum of three or more vectors to be performed in any sequence without altering the result.
For graphical understanding of associative addition, review Graphs Of Sine And Cosine Function.
FAQs on How to Add Three Vectors: Step-by-Step Guide
1. What is meant by the addition of three vectors?
Addition of three vectors means finding a single vector, called the resultant, that has the same effect as applying the three vectors one after another. The sum is found by connecting them head-to-tail in any order and drawing an arrow from the start of the first to the end of the last.
- Represent each vector graphically as an arrow.
- Place the tail of the second at the head of the first, and the third at the head of the second.
- The resultant is the vector from the tail of the first to the head of the last.
2. How do you add three vectors using the triangle or polygon law?
To add three vectors using the polygon (triangle) law, place the vectors in sequence head-to-tail and connect the start of the first to the end of the last.
- Draw the first vector accurately to scale and direction.
- From its tip, draw the second vector.
- From the tip of the second, draw the third vector.
- The vector from the start of the first to the end of the third is the resultant vector.
3. What are the analytical methods to add three vectors?
The analytical method of adding three vectors involves breaking each vector into its components along the axes, usually x and y.
- Write each vector in component form: V1 = (x1, y1), etc.
- Sum all x-components and all y-components separately.
- The resultant vector's components are Rx = x1+x2+x3, Ry = y1+y2+y3.
- Find the magnitude: √(Rx2 + Ry2), and direction using tan-1(Ry/Rx).
4. Can three vectors of different magnitudes give a zero resultant?
Yes, three vectors of different magnitudes can have a zero resultant if they form a closed triangle when placed head-to-tail.
- The condition is: The vectors must be able to form a triangle.
- Mathematically, the sum of any two vectors must be greater than or equal to the third.
- Otherwise, the resultant will not be zero.
5. State the conditions for the addition of three vectors to produce a null vector.
For three vectors to add up to zero (null vector), they must be represented as sides of a triangle taken in order.
- Vectors must be applied in sequence, head-to-tail.
- Final point must coincide with the starting point.
- This means the resultant is zero, and physically, the net effect cancels out.
6. What is the graphical method for the addition of three vectors?
The graphical method for adding three vectors involves drawing them to scale in a head-to-tail sequence and finding the resultant by measuring the line from start to end.
- Use a ruler and protractor for accuracy.
- Draw each vector in proper direction and length.
- The closing side of the polygon gives the resultant vector's magnitude and direction.
7. What are the steps to find the resultant of three vectors analytically?
Steps to find the resultant analytically:
- Resolve each vector into its components (x and y directions).
- Add corresponding components: Rx and Ry.
- Find magnitude: √(Rx2 + Ry2).
- Find direction: tan-1(Ry/Rx).
8. Why is the order of vector addition not important?
The order of vector addition is not important because of the commutative property of vectors.
- The resultant vector remains the same regardless of the order in which the vectors are added.
- This allows flexibility in calculations and graphical methods.
9. How do you represent the addition of three vectors mathematically?
Mathematically, the addition of three vectors is represented as:
R = A + B + C, where R is the resultant and A, B, C are the vectors.
- Each vector can be expressed in component form as (x, y).
- Add all corresponding components for the resultant.
- Final magnitude and direction are calculated from these components.
10. Explain, using an example, how to calculate the resultant of three vectors given their magnitudes and angles.
To calculate the resultant of three vectors with known magnitudes and angles:
- Resolve each vector into x and y components using the formulas: Vx = V cosθ, Vy = V sinθ.
- Add up all x-components and all y-components.
- Find the resultant's magnitude: √((ΣVx)2 + (ΣVy)2).
- Calculate direction using tan-1(ΣVy/ΣVx).


































