Question

Let \[A,B,C\] are three non-empty sets. If \[A\subset B\] and \[B\subset C\], then which of the following is true?
A. \[B-A=C-B\]
B. \[A\cap B\cap C=B\]
C. \[A\cup B=B\cap C\]
D. \[A\cup B\cup C=A\]

Answer 1

Hint: In this question, we are to find the true statements for the given three non-empty sets \[A, B, C\]. For this, a Venn diagram is used to represent the given conditions. So, that we can easily evaluate the given statements either to be true or false.



Formula Used:Set: A collection of objects in which it is possible to decide whether a given object belongs to the collection or not is said to be a set. Those objects are nothing but the elements in the set.
Sets are represented in two ways: The roaster method and the set builder form
Roaster method:
The set of vowels – \[\left\{ a,\text{ }e,\text{ }i,\text{ }o,\text{ }u \right\}\]
The set of natural numbers – \[\left\{ 1,\text{ }2,\text{ }3,\text{ }\ldots . \right\}\]
Set builder form:
The set of vowels – \[\left\{ x:x\text{ }is\text{ }a\text{ }vowel\text{ }in\text{ }English\text{ }alphabet \right\}\]
The set of natural numbers – \[\left\{ x:x\text{ }is\text{ }a\text{ }natural\text{ }number \right\}\]
Some of the important mathematical sets:
$N$ - the set of natural numbers - $N=\{1,2,3...\}$
$Z$- the set of integers - $Z=\{0,\pm 1,\pm 2,\pm 3,...\}$
If two sets $A, B$ where the set $A$ is said to be the subset of $B$ i.e., $A\subseteq B$ then every element of $A$ is in the set $B$ and the set $A$ is said to be the proper subset of $B$ i.e., \[A\subset B\] then $A\subseteq B$ and $A\ne B$.



Complete step by step solution:It is given that the three non-empty sets are \[A, B, C\]
And we have given that \[A\subset B\] and \[B\subset C\]
Then, the Venn diagram that represents the given sets is as follows:



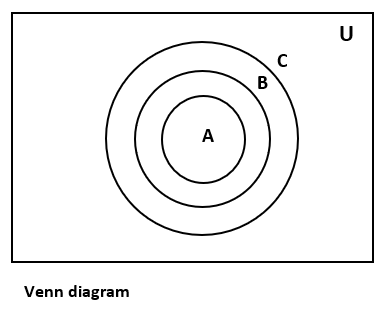
From the diagram, we can write
\[\begin{align}
  & B-A=B;A\subset B \\
 & C-B=C;B\subset C \\
\end{align}\]
So,
\[B-A\ne C-B\]
Thus, statement (1) is false.
Here we can write, \[A\cap B=A;A\subset B\]
Then,
\[(A\cap B)\cap C=A\cap C=A\]
So,
\[A\cap B\cap C\ne B\]
Thus, statement (2) is also false.
And
\[(A\cup B)=B;A\subset B\]
Then,
\[(A\cup B)\cup C=B\cup C=B\]
So,
\[A\cup B\cup C\ne A\]
Thus, statement (4) is also false.
Then from the Venn diagram, we have
$A\cup B=B;A\subset B$
And
\[B\cap C=B;B\subset C\]
So,
\[\begin{align}
  & A\cup B=B \\
 & B\cap C=B \\
 & \therefore A\cup B=B\cap C \\
\end{align}\]
Thus, statement (3) is true.



Option ‘C’ is correct



Note: Here we need to draw the Venn diagram according to the given conditions. So, that we can easily extract the correct statements for the given three non-empty sets.