Question

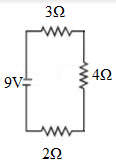
In circuit shown in figure the current through

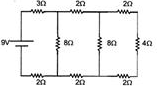
A. the \[3\Omega \] resistor is \[0.50A\]
B. the \[3\Omega \] resistor is \[0.25A\]
C .the \[4\Omega \] resistor is \[0.50A\]
D. the \[4\Omega \]resistor is \[0.25A\]

Answer 1

Hint: The resistor's voltage V in volts (V) divided by its resistance R in ohms (R) gives rise to the resistor's current I in amps (A): V is the voltage drop of the resistor, expressed in Volts (V). Voltage is sometimes represented by the letter E in Ohm's law.


Formula used:


Complete answer:
We have been provided in the question that the current through the circuit is,

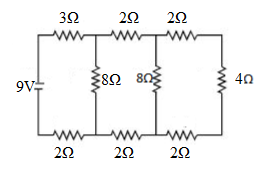
To begin, we will calculate the equivalent resistance of the resistors in the circle.

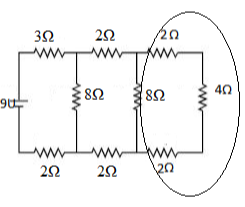
These resistances are connected in series. As a result, their equivalent resistance is equal to \[2\Omega + 4\Omega + 2\Omega = 8\Omega \] according to the formula. This equivalent resistor, together with the resistor in the box, yields an equivalent resistor of \[{\left( {\frac{1}{{8{\rm{\Omega }}}} + \frac{1}{{8{\rm{\Omega }}}}} \right)^{ - 1}} = 4{\rm{\Omega }}\]
This is depicted in the following figure.

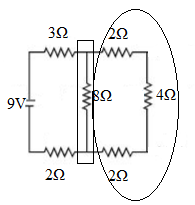
Repeating the process for the resistors in the circle and box, we get the equivalent resistance of the resistors in the circle as \[2\Omega + 4\Omega + 2\Omega = 8\Omega \], and the equivalent resistance of this and the resistor in the box as \[{\left( {\frac{1}{{8{\rm{\Omega }}}} + \frac{1}{{8{\rm{\Omega }}}}} \right)^{ - 1}} = 4{\rm{\Omega }}\].
This is depicted in the following figure.

We can observe that the overall resistance in the circuit is
\[2\Omega + 4\Omega + 3\Omega = 9\Omega \]
As per Ohm's law, the current flowing through in this circuit will now be
\[V = IR\]
On solving for I, we can write as
\[I = \frac{V}{R}\]
Now, we have to substitute the value we get
\[ = \frac{{9V}}{{9{\rm{\Omega }}}}\]
On simplifying the above equation, we get
\[ = 1A\]
Returning to the original circuit, the resistance on both routes is equal, therefore the current divides equally once more.

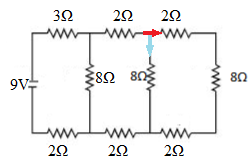
This gives us the current through the \[3\] ohm resistor as \[1\] amp and the current through the 4 ohm resistor as \[0.25\] amp
As a result, the current will be divided equally.
Hence, the option B is correct






Note: Keep in mind that current does not always split evenly between the two branches of the circuit. It is determined by the amount of resistance between them. The current was equally distributed in this case because the resistance on the different branches of the circuit was equal.