
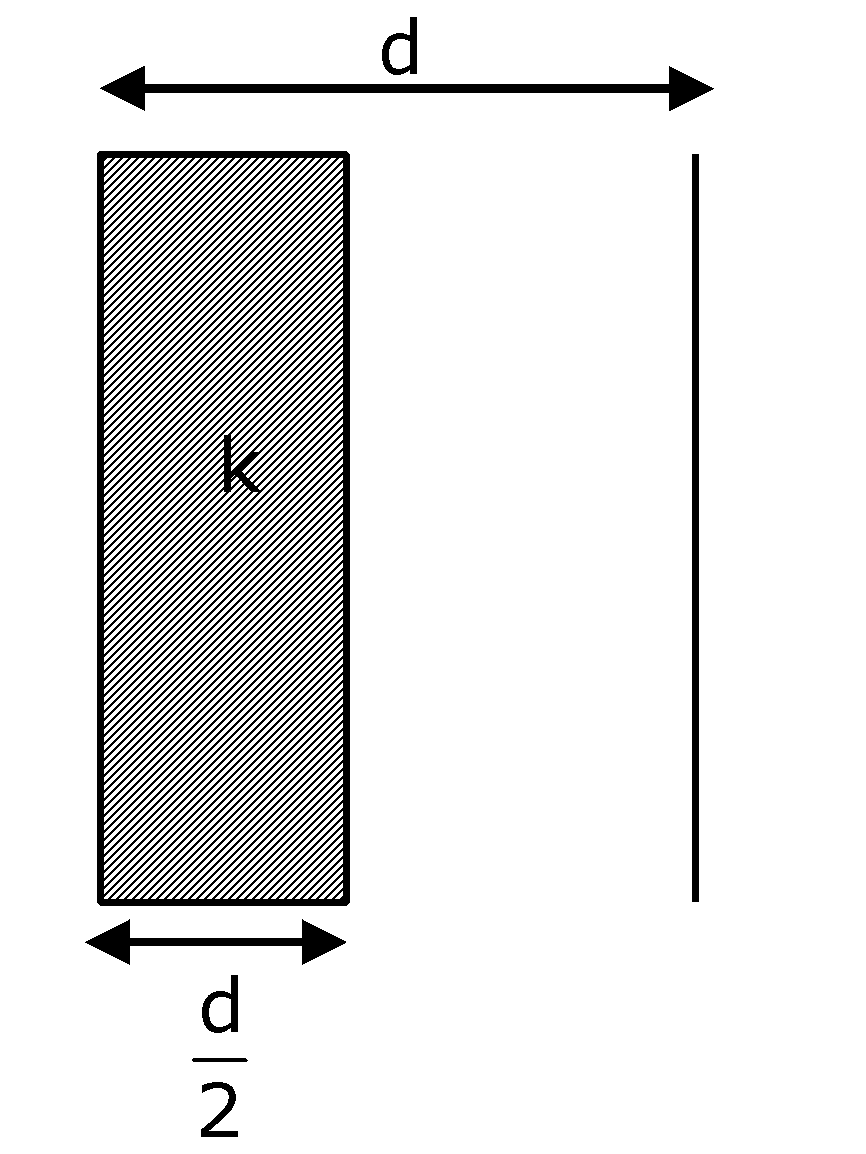
In a parallel plate capacitor set up, the plate area of the capacitor is 2 $m^2$ and the plates are separated by 1 m. If the space between the plates is filled with a dielectric material of thickness 0.5 m and area 2 $m^2$ (see fig) the capacitance of the set-up will be ________$\varepsilon_0$. (Dielectric constant of the material = 3.2) (Round off to the Nearest Integer)
Answer
225.6k+ views
Hint: In this problem, the capacitance of a parallel plate capacitor must be determined. $C=\dfrac{K{{\in }_{o}}A}{d}$ is the formula for a parallel plate capacitor. The net capacitance for capacitors connected in parallel is calculated using the formula \[{{C}_{net}}={C_1}+{C_2}\]. Additionally, the charge of a parallel plate capacitor is determined by$Q=CV$, and the parallel plate capacitor's electric field is determined by\[E=Vd\].
Complete answer:
The ratio of the magnitude of the charge on each conductor to the magnitude of the potential difference (PD) between them is known as the capacitance (C) of a capacitor.
Hence, we can say that capacitance is equal to the ratio charge is to potential difference.
The value of capacitance is always positive. The coulomb per volt or farad is the S.I. unit for capacitance (F).
The size, shape, relative placements of the plates, and the medium between them all affect the capacitance value. The charge on the plate or the distance between the plates has no bearing on the value of C.
The capacitor's capacitance is determined by $C=\dfrac{{{\varepsilon }_{0}}A}{d}$.
According to the question,
${{C}_{1}}=\dfrac{K{{\varepsilon }_{0}}A}{{d}/{2}\;}$ and ${{C}_{2}}=\dfrac{{{\varepsilon }_{0}}A}{{d}/{2}\;}$
OR
$C=\dfrac{{{E}_{0}}A}{\varepsilon \left( \dfrac{d}{K} \right)}=\dfrac{{{E}_{0}}A}{\dfrac{d}{2K}+\dfrac{d}{2}}$
Now,
$\dfrac{1}{C}=\dfrac{1}{{{C}_{1}}}+\dfrac{1}{{{C}_{2}}}$
$\Rightarrow \dfrac{1}{C}=\dfrac{d}{2K{{\varepsilon }_{0}}A}+\dfrac{d}{2{{\varepsilon }_{0}}A}$
$\Rightarrow \dfrac{1}{C}=\dfrac{2{{E}_{0}}AK}{d(K+1)}$
$\Rightarrow \dfrac{1}{C}=\dfrac{d}{2{{\varepsilon }_{0}}A}\left( \dfrac{K+1}{K} \right)$
$C=\dfrac{2{{\varepsilon }_{0}}AK}{d(K+1)}=\dfrac{2\times 2\times 3.2}{1\times 4.2}{{E}_{0}}$
$C=3.04{{E}_{0}}$
Hence, the answer is 3.04.
Note: Sparking occurs when the two capacitor plates are connected by a conducting wire, demonstrating the transformation of electrical energy into heat and light energy. If a medium with a dielectric constant of K is put between a capacitor's plates, the capacitance of the capacitor will increase K times.
Complete answer:
The ratio of the magnitude of the charge on each conductor to the magnitude of the potential difference (PD) between them is known as the capacitance (C) of a capacitor.
Hence, we can say that capacitance is equal to the ratio charge is to potential difference.
The value of capacitance is always positive. The coulomb per volt or farad is the S.I. unit for capacitance (F).
The size, shape, relative placements of the plates, and the medium between them all affect the capacitance value. The charge on the plate or the distance between the plates has no bearing on the value of C.
The capacitor's capacitance is determined by $C=\dfrac{{{\varepsilon }_{0}}A}{d}$.
According to the question,
${{C}_{1}}=\dfrac{K{{\varepsilon }_{0}}A}{{d}/{2}\;}$ and ${{C}_{2}}=\dfrac{{{\varepsilon }_{0}}A}{{d}/{2}\;}$
OR
$C=\dfrac{{{E}_{0}}A}{\varepsilon \left( \dfrac{d}{K} \right)}=\dfrac{{{E}_{0}}A}{\dfrac{d}{2K}+\dfrac{d}{2}}$
Now,
$\dfrac{1}{C}=\dfrac{1}{{{C}_{1}}}+\dfrac{1}{{{C}_{2}}}$
$\Rightarrow \dfrac{1}{C}=\dfrac{d}{2K{{\varepsilon }_{0}}A}+\dfrac{d}{2{{\varepsilon }_{0}}A}$
$\Rightarrow \dfrac{1}{C}=\dfrac{2{{E}_{0}}AK}{d(K+1)}$
$\Rightarrow \dfrac{1}{C}=\dfrac{d}{2{{\varepsilon }_{0}}A}\left( \dfrac{K+1}{K} \right)$
$C=\dfrac{2{{\varepsilon }_{0}}AK}{d(K+1)}=\dfrac{2\times 2\times 3.2}{1\times 4.2}{{E}_{0}}$
$C=3.04{{E}_{0}}$
Hence, the answer is 3.04.
Note: Sparking occurs when the two capacitor plates are connected by a conducting wire, demonstrating the transformation of electrical energy into heat and light energy. If a medium with a dielectric constant of K is put between a capacitor's plates, the capacitance of the capacitor will increase K times.
Recently Updated Pages
JEE Main 2025-26 Experimental Skills Mock Test – Free Practice

JEE Main 2025-26: Magnetic Effects of Current & Magnetism Mock Test

JEE Main 2025-26 Atoms and Nuclei Mock Test – Free Practice Online

JEE Main Mock Test 2025-26: Optics Chapter Practice Online

The work done in slowly moving an electron of charge class 12 physics JEE_Main

The value of the resistor RS needed in the DC voltage class 12 physics JEE_Main

Trending doubts
JEE Main 2026: City Intimation Slip and Exam Dates Released, Application Form Closed, Syllabus & Eligibility

JEE Main 2026 Application Login: Direct Link, Registration, Form Fill, and Steps

Understanding the Angle of Deviation in a Prism

Hybridisation in Chemistry – Concept, Types & Applications

How to Convert a Galvanometer into an Ammeter or Voltmeter

Ideal and Non-Ideal Solutions Explained for Class 12 Chemistry

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

JEE Advanced 2026 - Exam Date (Released), Syllabus, Registration, Eligibility, Preparation, and More

JEE Advanced 2026 - Exam Date (Released), Syllabus, Registration, Eligibility, Preparation, and More

Dual Nature of Radiation and Matter Class 12 Physics Chapter 11 CBSE Notes - 2025-26

Understanding Atomic Structure for Beginners

Understanding Electromagnetic Waves and Their Importance




