Question

If in the $\triangle ABC, AB = 2BC$, then $tan\dfrac{B}{2}:cot(\dfrac{C-A}{2})$
A. 3:1
B. 2:1
C. 1:2
D. 1:3

Answer 1

Hint: We are given $\triangle ABC$ with $AB = 2BC$, we need to find the ratio $tan\dfrac{B}{2}:cot(\dfrac{C-A}{2})$. Recall the law of sins and the trigonometric identities. We use these concepts to solve the question.

Formula Used: - Law of sines,
$\dfrac{sin A}{a} = \dfrac{sin B}{b} = \dfrac{sin C}{c}$
- $tan(90^{\circ} - x) = cot x$
-$sin(x-y)+sin(x+y) = 2sinxcosy$

Complete step by step solution: We have $\triangle ABC$ with $AB = 2BC$. We need to find the ratio between $tan \dfrac{B}{2}$ and $cot (\dfrac{C-A}{2})$.
We know that the angles of a triangle are supplementary. Therefore, we have
$\angle A+\angle B+\angle C = 180^{\circ}$
$\angle B = 180^{\circ}-(\angle C +\angle A)$
$\dfrac{\angle B}{2} = \dfrac{180^{\circ}-(\angle C+\angle A)}{2}$
$\dfrac{\angle B}{2} = 90^{\circ}-\dfrac{(\angle C + \angle A)}{2}$
$\therefore tan\dfrac{B}{2} = tan~(90^{\circ}-\dfrac{(\angle C + \angle A)}{2})$
$\implies tan \dfrac{B}{2} = cot(\dfrac{(C + A)}{2})$
Now,
$\dfrac{tan \dfrac{B}{2}}{cot(\dfrac{C-A}{2})} =\dfrac{cot(\dfrac{(C + A)}{2})}{cot(\dfrac{(C-A)}{2})}$
$\implies \dfrac{tan \dfrac{B}{2}}{cot(\dfrac{(C-A)}{2})} = cot(\dfrac{(C + A)}{2})tan(\dfrac{(C-A)}{2})$
$\implies \dfrac{tan \dfrac{B}{2}}{cot(\dfrac{(C-A)}{2})} = \dfrac{cos(\dfrac{(C + A)}{2})sin(\dfrac{(C-A)}{2})}{sin(\dfrac{(C + A)}{2})cos(\dfrac{(C-A)}{2})}$
$\implies \dfrac{tan \dfrac{B}{2}}{cot(\dfrac{(C-A)}{2})} = \dfrac{2cos(\dfrac{(C + A)}{2})sin(\dfrac{(C-A)}{2})}{2sin(\dfrac{(C + A)}{2})cos(\dfrac{(C-A)}{2})}$
$\implies \dfrac{tan \dfrac{B}{2}}{cot(\dfrac{(C-A)}{2})} = \dfrac{2sin(\dfrac{(C-A)}{2})cos(\dfrac{(C + A)}{2})}{2sin(\dfrac{(C + A)}{2})cos(\dfrac{(C-A)}{2})}$
By using the equation,$sin(x-y)+sin(x+y) = 2sinxcosy$ we simplify the numerator and denominator.
$\implies \dfrac{tan \dfrac{B}{2}}{cot(\dfrac{(C-A)}{2})} = \dfrac{sin(\dfrac{(C-A)}{2}-\dfrac{(C + A)}{2}))+sin(\dfrac{(C-A)}{2}+\dfrac{(C + A)}{2}}{sin(\dfrac{(C + A)}{2})- \dfrac{(C-A)}{2})+sin (\dfrac{(C + A)}{2})+ \dfrac{(C-A)}{2})}$
$\implies \dfrac{tan \dfrac{B}{2}}{cot(\dfrac{(C-A)}{2})} =\dfrac{sin(\dfrac{C-A-C-A}{2})+sin(\dfrac{C-A+C+A}{2})}{sin(\dfrac{C+A-C+A}{2})+sin(\dfrac{C+A+C-A}{2})}$
$\implies \dfrac{tan \dfrac{B}{2}}{cot(\dfrac{(C-A)}{2})} =\dfrac{sin(\dfrac{-2A}{2})+sin(\dfrac{2C}{2})}{sin(\dfrac{2A}{2})+sin(\dfrac{2C}{2})}$
$\implies \dfrac{tan \dfrac{B}{2}}{cot(\dfrac{(C-A)}{2})} =\dfrac{sin(-A)+sin(C)}{sin(A)+sin(C)}$
$\implies \dfrac{tan \dfrac{B}{2}}{cot(\dfrac{(C-A)}{2})} =\dfrac{sin(C)-sin(A)}{sin(C)+sin(A)}$
$\implies \dfrac{tan \dfrac{B}{2}}{cot(\dfrac{(C-A)}{2})} =\dfrac{\dfrac{sin(C)}{sin A}-1}{\dfrac{sin(C)}{sin(A)}+1}$ --(1)
By using the law of sines,

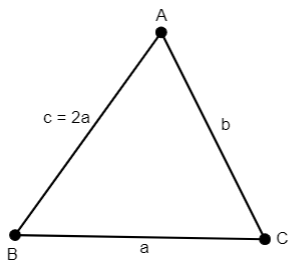
$\dfrac{sin A}{a} = \dfrac{sin B}{b} = \dfrac{sin C}{c}$
We are given that $AB = 2BC$,
$\therefore c = 2a$
Therefore, we get
$\dfrac{sin A}{a} = \dfrac{sin B}{b} = \dfrac{sin C}{2a}$
$\implies \dfrac{sin A}{a} =\dfrac{sin C}{2a}$
$\dfrac{sin C}{sin A} = \dfrac{2a}{a}$
$\implies \dfrac{sin C}{sin A} = 2$
Substituting the above equation in (1) we get,
$\dfrac{tan \dfrac{B}{2}}{cot(\dfrac{(C-A)}{2})} =\dfrac{2-1}{2+1}$
$\therefore \dfrac{tan \dfrac{B}{2}}{cot(\dfrac{(C-A)}{2})} =\dfrac{1}{3}$
$\implies tan\dfrac{B}{2} : cot(\dfrac{C-A}{2}) = 1:3$

So, Option ‘D’ is correct

Note: We can solve this question by using the Naiper's Analogy. There are three equations in Naiper's Analogy,
$tan(\dfrac{A-B}{2}) = \dfrac{a-b}{a+b}cot(\dfrac{C}{2})$
$tan(\dfrac{B-C}{2}) = \dfrac{b-c}{b+c}cot(\dfrac{A}{2})$
$tan(\dfrac{C-A}{2}) = \dfrac{c-a}{c+a}cot(\dfrac{B}{2})$
Modify the last equation,
$\dfrac{1}{cot(\dfrac{B}{2})} = \dfrac{c-a}{c+a}\dfrac{1}{tan(\dfrac{C-A}{2})}$
$\implies tan(\dfrac{B}{2}) = \dfrac{c-a}{c+a}cot(\dfrac{C-A}{2})$
Now applying $c = 2a$, we get the required ratio.