Question

If at angle θ the light takes maximum time to travel in optical fiber. Then the maximum time is $y\times {{10}^{-8}}s$, calculate $y$. (n1=1.44 , n2=1.5)

Answer 1

Hint:In this question we will use the concept of Snell’s law. According to Snell's law, for light of a particular colour and for the given pair of media, the ratio of the sine of the angle of incidence to the sine of the angle of refraction is a constant.




Formula used:
Snell’s Law: ${{n}_{1}}\sin ({{\theta }_{1}})={{n}_{2}}\sin ({{\theta }_{2}})$, where ${{n}_{1}}$=refractive index of medium 1, ${{n}_{2}}$= refractive index of medium 2, ${{\theta }_{1}}$=angle of incidence and ${{\theta }_{2}}$= angle of refraction





Complete answer:

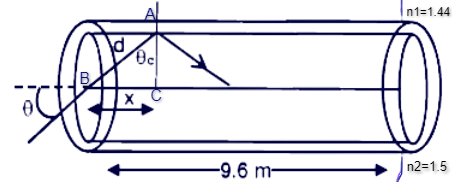
For the ray to take maximum time to cross the optical fiber, it has to have distance covered greater than displacement, that is it will travel making multiple triangles as shown in the picture above, and not in a straight line.

Let AB=d and BC=x
If the incident angle is θ then angle ABC is also equal to θ by geometry.
Applying Snell’s law at point A, for finding critical angle (θc)
${{n}_{2}}\sin ({{\theta }_{c}})={{n}_{1}}\sin (\theta )$
$\Rightarrow 1.5\sin ({{\theta }_{c}})=1.44\sin ({{90}^{\circ }})$
$\Rightarrow \sin ({{\theta }_{c}})=\dfrac{1.44}{1.5}=\dfrac{24}{25}$ - (1)
In triangle ABC,
$\sin ({{\theta }_{c}})=\dfrac{x}{d}$
And by equation (1) we have
$\dfrac{x}{d}=\dfrac{24}{25}$
$\Rightarrow d=\dfrac{25x}{24}$
For displacement x the distance covered by the ray is equal to d, where $d=\dfrac{25x}{24}$
Therefore, for displacement = 9.6m, the distance covered by the ray = $\dfrac{25\times 9.6}{24}=10m$
Now, the speed of light in the denser medium = $\dfrac{c}{{{n}_{2}}}=\dfrac{3\times {{10}^{8}}}{1.5}$
Time taken by the ray to travel 10m distance inside the optical fiber=$\dfrac{distance\text{ }travelled}{speed\text{ }of\text{ }light\text{ }in\text{ }that\text{ }medium}=\dfrac{10}{\dfrac{3\times {{10}^{8}}}{1.5}}$
$\Rightarrow Time\text{ }taken=5\times {{10}^{-8}}s$
Therefore, y=5

The correct answer is 5.


Note:The maximum angle at which a light beam traveling through one transparent material can encounter the surface of another with a lower refractive index without being completely reflected within the first medium is known as the critical angle in optics. The value of angle of refraction is ${{90}^{\circ}}$, when angle of incidence becomes critical angle.