Question

If \[A = B + C\] and the value of A, B, and C are 13, 12, and 5 respectively, then find the angle between A and C.
A.\[{\cos ^{ - 1}}\left( {\dfrac{5}{{13}}} \right)\]
B. \[{\cos ^{ - 1}}\left( {\dfrac{{13}}{{12}}} \right)\]
C. \[\dfrac{\pi }{2}\]
D. \[{\sin ^{ - 1}}\left( {\dfrac{5}{{12}}} \right)\]

Answer 1

Hints First we will apply the Pythagorean theorem to check whether the given triangle is a right-angle triangle or not. Then decide which are the legs and hypotenuse of the triangle. Then find the angle between B and C using the trigonometry ratios.

Formula used
The Pythagoras theorem for right angle is,
\[{a^2} + {b^2} = {c^2}\], where a is the base, b is the height, and c is the hypotenuse.
Also,
\[\cos \theta = \dfrac{p}{q}\], where p is the base and q is the hypotenuse.

Complete step by step solution
The given lengths of the sides are 13, 12, and 5.
Now,
\[{12^2} + {5^2}\]
\[ = 144 + 25\]
\[ = 169\]
\[ = {13^2}\]
Therefore, according to Pythagoras' theorem, the given triangle is right-angled.
The diagram of the given triangle is,

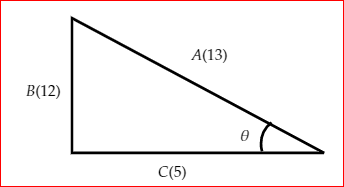
Use the formula \[\cos \theta = \dfrac{p}{q}\] , where p is the base and q is the hypotenuse to obtain the required result.
Therefore,
\[\cos \theta = \dfrac{5}{{13}}\]
\[\theta = {\cos ^{ - 1}}\left( {\dfrac{5}{{13}}} \right)\] .

The correct option is A.

Note Students often used cosine formula \[{A^2} = {B^2} + {C^2} + 2BC\cos \phi \] to obtain the angle between B and C and \[\theta\]. By using the cosine formula we cannot able find the angle between B and C. Because the cosine formula is applicable to an oblique triangle. Thus we will use trigonometry ratios to find the angle between them.