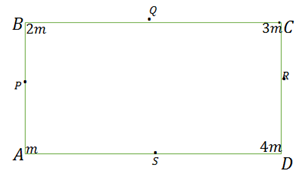Answer
91.5k+ views
Hint: A vertex (plural: vertices) is where at least two line portions meet. It is a Corner. This tetrahedron has 4 vertices.
All shapes are composed of lines. These lines are called sides.
A vertex is where different sides meet, similar to a corner. A square has 4 sides and 4 vertices. In calculation, a square is a normal quadrilateral, which implies that it has four equivalent sides and four equivalent points.
It can likewise be characterized as a square shape wherein two contiguous sides have equivalent length. A square with vertices would be signified.
A square is an exceptional instance of a rhombus (equivalent sides, inverse equivalent points), a kite (two sets of nearby equivalent sides), a trapezoid (one set of inverse sides equal), a parallelogram (all contrary sides equal), a quadrilateral or tetragon (four-sided polygon), and a square shape (inverse sides equivalent, right-points), and subsequently has all the properties of every one of these shapes.
Formula used:
Distance of new position t0 center of mass from its old position is \[AP = AB\]
$ = \sqrt {{{\left( {X - {X_1}} \right)}^2} + {{\left( {Y - {Y_1}} \right)}^2}} $
Complete step by step answer:
Let our new point is \[M\] an old point is\[N\]
four particles of masses $m$,$2m$,$3m$ and $4m$
Let com be \[M\left( {X,Y} \right)\]
For \[X\] point
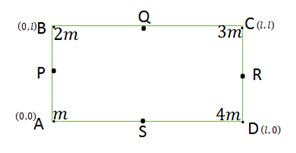
\[X = \dfrac{{m \times 0 + 2m \times 0 + 3m \times l + 4m \times l}}{{m + 2m + 3m + 4m}}\]
Simplifying we get,
$ \Rightarrow \dfrac{{7ml}}{{10m}}$
$ \Rightarrow \dfrac{7}{{10}}l$
Then, similarly
For \[Y\] point
\[Y\]\[ = \dfrac{{2m \times 0 + 3m \times l + 4m \times l + m \times 0}}{{m + 2m + 3m + 4m}}\]
Simplifying we get,
$ \Rightarrow \dfrac{{5ml}}{{10m}}$
$ \Rightarrow \dfrac{5}{{10}}l$
Now the particles $A,B,C$ and $D$ are displaced to their new position $B,C,D,A$ respectively $ABCD \to BCDA$
Let new position be \[N\left( {X,Y} \right)\]
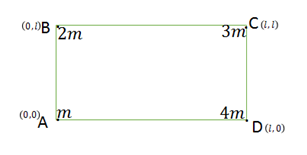
\[X\]\[ = \dfrac{{2m \times 0 + 3m \times 0 + 4m \times l + m + l}}{{m + 2m + 3m + 4m}}\]
Simplifying we get,
$ \Rightarrow \dfrac{{5ml}}{{10m}}$
$ \Rightarrow \dfrac{5}{{10}}l$
Then, similarly
For \[Y\] point
$Y$\[ = \dfrac{{2m \times 0 + 3m \times l + 4m \times l + m \times 0}}{{m + 2m + 3m + 4m}}\]
Simplifying we get,
$ \Rightarrow \dfrac{{7ml}}{{10m}}$
$ \Rightarrow \dfrac{7}{{10}}l$
Distance of new position \[M\] to the center of mass from its old position \[N\] is,
$ \Rightarrow \sqrt {{{\left( {X - {X_1}} \right)}^2} + {{\left( {Y - {Y_1}} \right)}^2}} $$l$
Substituting,
$ \Rightarrow \sqrt {{{\left( {\dfrac{7}{{10}} - \dfrac{5}{{10}}} \right)}^2} + {{\left( {\dfrac{5}{{10}} - \dfrac{7}{{10}}} \right)}^2}{l^2}} $$\left( B \right)$
Subtracting and squaring the terms,
$ \Rightarrow \sqrt {\left( {\dfrac{4}{{100}}} \right) + {{\left( {\dfrac{4}{{100}}} \right)}^{}}} $$l$
Adding the terms,
$ \Rightarrow \sqrt {\left( {\dfrac{8}{{100}}} \right)} $$l$
Taking square root,
$ \Rightarrow \dfrac{{2\sqrt 2 }}{{10}}l$
$ \Rightarrow \dfrac{{\sqrt 2 }}{5}l$
Hence the answer is $\left( B \right)$
Note: The components of the square are found by figuring the separation between different corner focuses. Review that we can discover the separation between any two focuses on the off chance that we know their directions. (See Distance between Two Points) So in the figure above:
The length of each side of the square is the separation of any two neighboring focuses (state, or)
The length of a diagonal is the separation between inverse corners, state, or potentially since the diagonals are compatible).
This strategy will work regardless of whether the square is turned on the plane (click on "pivoted" previously). In any case, if the sides of the square are corresponding to the and tomahawks, at that point the estimations can be somewhat simpler.
In the above figure uncheck the "pivoted" box and note that The side length is the distinction in directions of any left and right point - for instance.
All shapes are composed of lines. These lines are called sides.
A vertex is where different sides meet, similar to a corner. A square has 4 sides and 4 vertices. In calculation, a square is a normal quadrilateral, which implies that it has four equivalent sides and four equivalent points.
It can likewise be characterized as a square shape wherein two contiguous sides have equivalent length. A square with vertices would be signified.
A square is an exceptional instance of a rhombus (equivalent sides, inverse equivalent points), a kite (two sets of nearby equivalent sides), a trapezoid (one set of inverse sides equal), a parallelogram (all contrary sides equal), a quadrilateral or tetragon (four-sided polygon), and a square shape (inverse sides equivalent, right-points), and subsequently has all the properties of every one of these shapes.
Formula used:
Distance of new position t0 center of mass from its old position is \[AP = AB\]
$ = \sqrt {{{\left( {X - {X_1}} \right)}^2} + {{\left( {Y - {Y_1}} \right)}^2}} $
Complete step by step answer:
Let our new point is \[M\] an old point is\[N\]
four particles of masses $m$,$2m$,$3m$ and $4m$
Let com be \[M\left( {X,Y} \right)\]
For \[X\] point

\[X = \dfrac{{m \times 0 + 2m \times 0 + 3m \times l + 4m \times l}}{{m + 2m + 3m + 4m}}\]
Simplifying we get,
$ \Rightarrow \dfrac{{7ml}}{{10m}}$
$ \Rightarrow \dfrac{7}{{10}}l$
Then, similarly
For \[Y\] point
\[Y\]\[ = \dfrac{{2m \times 0 + 3m \times l + 4m \times l + m \times 0}}{{m + 2m + 3m + 4m}}\]
Simplifying we get,
$ \Rightarrow \dfrac{{5ml}}{{10m}}$
$ \Rightarrow \dfrac{5}{{10}}l$
Now the particles $A,B,C$ and $D$ are displaced to their new position $B,C,D,A$ respectively $ABCD \to BCDA$
Let new position be \[N\left( {X,Y} \right)\]
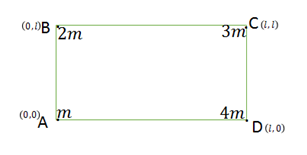
\[X\]\[ = \dfrac{{2m \times 0 + 3m \times 0 + 4m \times l + m + l}}{{m + 2m + 3m + 4m}}\]
Simplifying we get,
$ \Rightarrow \dfrac{{5ml}}{{10m}}$
$ \Rightarrow \dfrac{5}{{10}}l$
Then, similarly
For \[Y\] point
$Y$\[ = \dfrac{{2m \times 0 + 3m \times l + 4m \times l + m \times 0}}{{m + 2m + 3m + 4m}}\]
Simplifying we get,
$ \Rightarrow \dfrac{{7ml}}{{10m}}$
$ \Rightarrow \dfrac{7}{{10}}l$
Distance of new position \[M\] to the center of mass from its old position \[N\] is,
$ \Rightarrow \sqrt {{{\left( {X - {X_1}} \right)}^2} + {{\left( {Y - {Y_1}} \right)}^2}} $$l$
Substituting,
$ \Rightarrow \sqrt {{{\left( {\dfrac{7}{{10}} - \dfrac{5}{{10}}} \right)}^2} + {{\left( {\dfrac{5}{{10}} - \dfrac{7}{{10}}} \right)}^2}{l^2}} $$\left( B \right)$
Subtracting and squaring the terms,
$ \Rightarrow \sqrt {\left( {\dfrac{4}{{100}}} \right) + {{\left( {\dfrac{4}{{100}}} \right)}^{}}} $$l$
Adding the terms,
$ \Rightarrow \sqrt {\left( {\dfrac{8}{{100}}} \right)} $$l$
Taking square root,
$ \Rightarrow \dfrac{{2\sqrt 2 }}{{10}}l$
$ \Rightarrow \dfrac{{\sqrt 2 }}{5}l$
Hence the answer is $\left( B \right)$
Note: The components of the square are found by figuring the separation between different corner focuses. Review that we can discover the separation between any two focuses on the off chance that we know their directions. (See Distance between Two Points) So in the figure above:
The length of each side of the square is the separation of any two neighboring focuses (state, or)
The length of a diagonal is the separation between inverse corners, state, or potentially since the diagonals are compatible).
This strategy will work regardless of whether the square is turned on the plane (click on "pivoted" previously). In any case, if the sides of the square are corresponding to the and tomahawks, at that point the estimations can be somewhat simpler.
In the above figure uncheck the "pivoted" box and note that The side length is the distinction in directions of any left and right point - for instance.
Recently Updated Pages
Name the scale on which the destructive energy of an class 11 physics JEE_Main

Write an article on the need and importance of sports class 10 english JEE_Main

Choose the exact meaning of the given idiomphrase The class 9 english JEE_Main

Choose the one which best expresses the meaning of class 9 english JEE_Main

What does a hydrometer consist of A A cylindrical stem class 9 physics JEE_Main

A motorcyclist of mass m is to negotiate a curve of class 9 physics JEE_Main

Other Pages
The vapour pressure of pure A is 10 torr and at the class 12 chemistry JEE_Main

Electric field due to uniformly charged sphere class 12 physics JEE_Main

3 mole of gas X and 2 moles of gas Y enters from the class 11 physics JEE_Main

If a wire of resistance R is stretched to double of class 12 physics JEE_Main

Derive an expression for maximum speed of a car on class 11 physics JEE_Main

Velocity of car at t 0 is u moves with a constant acceleration class 11 physics JEE_Main