Question

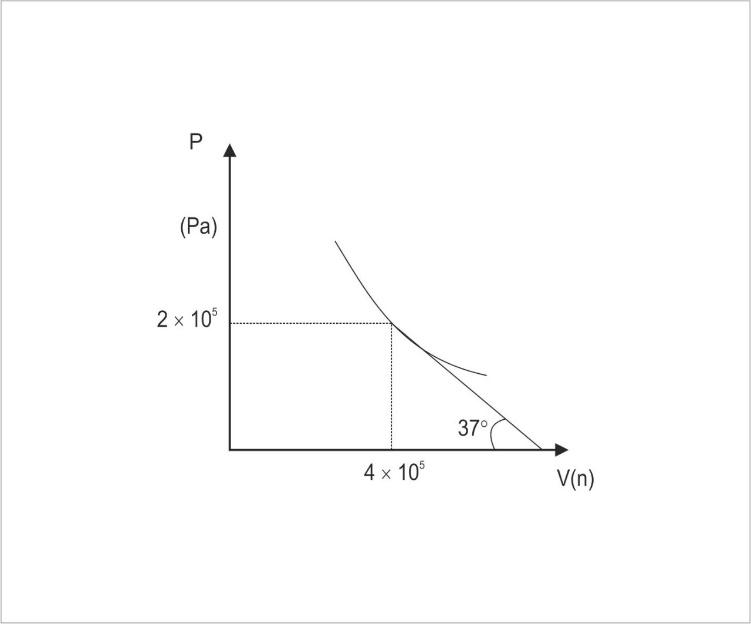
For an ideal gas $P$-$V$ graph undergoing polytropic process $P{V^m}$ = constant is shown here. Find the value of $m$.

Answer 1

Hint: In this question, first discuss the polytropic process and then discuss whether it is an adiabatic process or not. Discuss also for the different values of polytropic index how pressure, temperature, volume remains constant. Then differentiate the relation of a polytropic process and find out the value of $m$.

Complete step by step solution:
A polytropic process is a thermodynamic process which obeys the relation $P{V^n} = c$
Where, $p$ is the pressure, $V$ is the volume, and $n$ is the polytropic index.
In the case of a polytropic process heat transfer may occur or may not occur but in adiabatic process there is no heat transfer takes place so we can say that a polytropic process may be or may not be a adiabatic process.
Here it is given that polytropic process $P{V^m} = c$
We will differentiate both the side of the equation as,
$ \Rightarrow P \times m{V^{m - 1}}dV + {V^m}dP = 0$
Now, we will simplify the above expression as,
$ \Rightarrow m{V^{m - 1}}dV = - {V^m}dP$
After simplification we get,
$ \Rightarrow \dfrac{{dP}}{{dV}} = - \dfrac{{mP}}{V}......\left( 1 \right)$
From the given graph, we will calculate the slope of the curve as.
$ \Rightarrow \dfrac{{dP}}{{dV}} = \tan \left( {180^\circ - 37^\circ } \right)$
Now, simplify the above expression as,
$ \Rightarrow \dfrac{{dP}}{{dV}} = \tan 143^\circ $
After simplification we will get the value of the slope as,
$ \Rightarrow \dfrac{{dP}}{{dV}} = - 0.75$
In the question we have given Pressure $P$ as $2 \times {10^5}\;{\text{Pa}}$ and the volume as $4 \times {10^5}\;{{\text{m}}^3}$.
Now we calculate the value of $m$ by substituting the value in equation (1) as,
$ \Rightarrow - 0.75 = - \dfrac{{m \times 2 \times {{10}^5}}}{{4 \times {{10}^5}}}$
After simplification we will get.
$\therefore m = 1.5$

Thus, the value of $m$ is $1.5$.

Note: As we know that, in a polytropic process when the polytropic index $n = 1$ then the temperature remains constant in the process and when the polytropic index $n = \infty $ then the volume remains constant in the process. When the value of the polytropic index $n = 0$ then the pressure remains constant in the process and then we can say it is equivalent to an isobaric process.