Question

For a certain atom, there are energy levels A, B, C of a certain atom corresponds to increasing values of energy, i.e., \[{E_{A}} < {E_B} < {E_C}\] ​. Choose the correct option if \[{\lambda _1}\] \[,{\lambda _{2\;}}and\;{\lambda _3}\]​ are the wavelengths of radiations corresponding to the transitions C to B, B to A and C to A respectively:

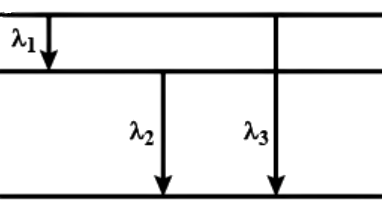
A. ${\lambda _3} = {\lambda _2} + {\lambda _1}$
B. ${\lambda _3} = \dfrac{{{\lambda _1}{\lambda _2}}}{{{\lambda _1} + {\lambda _2}}}$
C. ${\lambda _1} + {\lambda _2} + {\lambda _3} = 0$
D. $3{\lambda _2} = {\lambda _3} + 2{\lambda _1}$

Answer 1

Hint:The Neil Bohr’s gives us three postulates for hydrogen atoms. Think about the third postulates of Bohr’s model. An electron may only jump from one non-radiating orbit to another by emitting or absorbing energy. When an electron jumps from the inner to the outer orbit, it absorbs the difference between the total energy in the two stationary orbits, and when they jump from the outer to the inner orbit, they emit it.

Formula used:
$E = \dfrac{{hc}}{\lambda }$ .
where E is the energy, h is the planck's constant, c is the speed of light and greek letter lambda denotes the wavelength.

Complete step by step solution:
The Neil Bohr Model has three Bohr's Postulates, here the third postulate is explained in more detail below: Only when an electron jumps from one non-radiating orbit to another does energy either emit or absorb. When an electron jumps from the inner to the outer orbit, the energy difference between the two stationary orbits is absorbed, and when an electron jumps from the outer to the inner orbit, it is expelled.

If $E_1$ and $E_2$ are equal to the total energy (T.E.) of an e- in its inner and outer stationary orbits, respectively, the frequency of radiation released during a jump from the outer to the inner orbit is given by:
\[\;E{\text{ }} = \;{\text{ }}hf\;{\text{ }} = {\text{ }}{E_2} - {\text{ }}{E_1} \ldots .\left( 3 \right)\]
We are aware that the majority of hydrogen atoms exist in the ground state, and that when this atom is exposed to energy from an electron collision or heat, the electrons may need to be raised to a higher energy level, such as from n = 1 to n = 2, 3, etc. The difference between their energies may be determined using equation (3).

Now, we can write from equation (3):
${E_{2 \to 1}} = {E_{3 \to 1}} - {E_{3 \to 2}}$
If we apply $E = hf = \dfrac{{hc}}{\lambda }$. Then we get
$\dfrac{1}{{{\lambda _1}}} = \dfrac{1}{{{\lambda _3}}} - \dfrac{1}{{{\lambda _2}}}$
We can also write,
$\dfrac{1}{{{\lambda _3}}} = \dfrac{1}{{{\lambda _1}}} + \dfrac{1}{{{\lambda _2}}} = \dfrac{{{\lambda _1} + {\lambda _2}}}{{{\lambda _1}{\lambda _2}}}$
$\therefore {\lambda _3} = \dfrac{{{\lambda _1}{\lambda _2}}}{{{\lambda _1} + {\lambda _2}}}$

Therefore, option B is the correct answer.

Notes If you're wondering what these energy levels are, they are the fixed intervals around an atom's nucleus where it's possible to find electrons. One may relate energy levels to stair steps. The electrons can exist at either energy level, but not in the middle.