Question

Find the parametric form of the equation of the circle ${{x}^{2}}+{{y}^{2}}+px+py=0$.

Answer 1

Hint: To convert from the general form to the parametric form of the equation of a circle, all we have to do is find the centre of the circle and the radius.

$\begin{align}
  & x=r\cos t+{{x}_{0}} \\
 & y=r\sin t+{{y}_{0}} \\
\end{align}$ is the parametric equation of a circle whose centre is $({{x}_{0}},{{y}_{0}})$, and radius is $r$.
Parametric form of a circle is a way to express the general formula of any point lying on that circle in terms of the circle’s radius, centre’s coordinates, and an angle $\theta $.



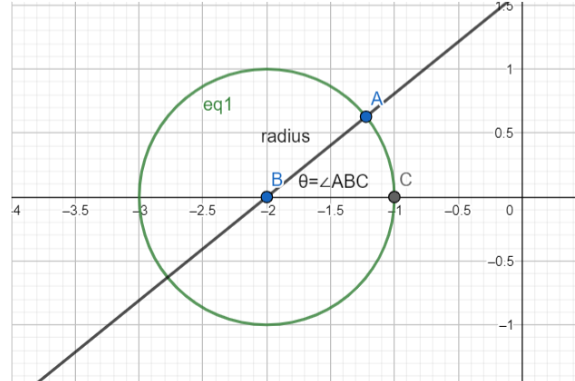
In the above figure, let’s consider $A$ to be the point that we want to express as a general point lying on the circle.
We know that, length of $AB$= radius of the circle
And, $\theta =\angle ABC$.
Let the coordinates of point $A=(X,Y)$
The equation of the circle drawn here is : ${{x}^{2}}+{{y}^{2}}+4x+3=0$. ……………...(1)
From here, if we compare it with the general equation of a circle which is :
${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$, we get :
$\begin{align}
  & 2gx=4x \\
 & \Rightarrow 2g=4 \\
 & \Rightarrow g=2 \\
 \end{align}$
And, $\begin{align}
 & 2fy=0 \\
 & \Rightarrow 2f=0 \\
& \Rightarrow f=0 \\
 \end{align}$
Since, we know that, the centre of the circle having the general equation = $(-g,-f)$, and radius = $\sqrt{{{g}^{2}}+{{f}^{2}}-c}$, we can compare again and find that :
Centre of the circle (1) drawn here, $C=(-g,-f)=(-2,0)$
And its radius, $r=\sqrt{{{g}^{2}}+{{f}^{2}}-c}=\sqrt{{{2}^{2}}-3}=1$
Hence, for the point $(X,Y)$ or $A$, we can say that :
$\sqrt{{{(X-(-2))}^{2}}+{{(Y-0)}^{2}}}=r=1$
Or, we can drop a perpendicular from $A$ to the line $BC$, and form a right angled triangle. Let’s call the point where the perpendicular is dropped, $D$.



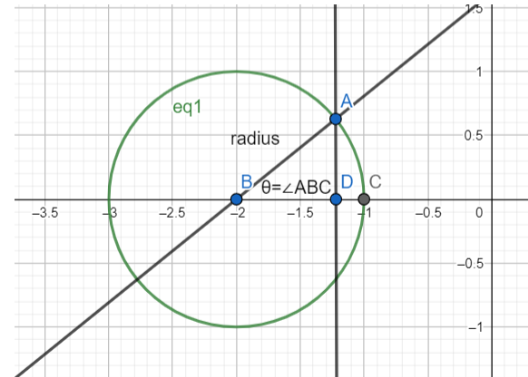
From the triangle $ABD$, we can conclude that, since it’s a right angled triangle,
$\cos \theta =\dfrac{BD}{AB}$ , and $\sin \theta =\dfrac{AD}{AB}$
$\begin{align}
  & \Rightarrow BD=AB\cos \theta \\
 & \Rightarrow BD=r\cos \theta \\
 & \Rightarrow (Y-0)=r\cos \theta \\
 & \Rightarrow Y=r\cos \theta \\
\end{align}$ and \[\begin{align}
  & \Rightarrow AD=AB\sin \theta \\
 & \Rightarrow AD=r\sin \theta \\
 & \Rightarrow (X-(-2))=r\sin \theta \\
 & \Rightarrow X+2=r\sin \theta \\
 & \Rightarrow X=r\sin \theta -2 \\
\end{align}\]
We have substituted the length of $AB$ as the radius of the circle, as shown in the diagram, and later substituted for the lengths of $BD$ and $AD$ by finding the difference of only the $x$ and $y$ coordinates at one time.
Hence, we can now write that the general point $A=(X,Y)=(r\sin \theta -2,r\cos \theta )$.
This form of expressing a point in the parametric form is called so since the parameters here are the angle the point makes with the $x$ axis and the radius of the circle.

Applying this knowledge in the question given to us, we’ll proceed stepwise.
First, let’s compare the equation ${{S}_{1}}={{x}^{2}}+{{y}^{2}}+px+py=0$ with the general equation ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$. Doing so, we get :
$\begin{align}
  & 2gx=px \\
 & \Rightarrow 2g=p \\
 & \Rightarrow g=\dfrac{p}{2} \\
\end{align}$ and $\begin{align}
  & 2fy=py \\
 & \Rightarrow 2f=p \\
 & \Rightarrow f=\dfrac{p}{2} \\
\end{align}$
The centre of circle ${{S}_{1}},{{C}_{1}}=(-g,-f)=(-\dfrac{p}{2},-\dfrac{p}{2})$
And the radius, ${{r}_{1}}=\sqrt{{{g}^{2}}+{{f}^{2}}-c}=\sqrt{\dfrac{{{p}^{2}}}{4}+\dfrac{{{p}^{2}}}{4}}=\sqrt{\dfrac{{{p}^{2}}}{2}}=\dfrac{p}{\sqrt{2}}$
To express the general point on this circle in terms of parameters the radius and the angle made with the $x$ axis, we assume it makes an angle $t$, since this angle varies according to the point’s position on the circle, but the radius remains fixed because a circle is a collection of points that have a fixed distance from a particular point.
Hence, the parametric equation of the circle is :
$\begin{align}
  & x={{r}_{1}}\cos t+g \\
 & y={{r}_{1}}\sin t+f \\
\end{align}$
Where, $(x,y)$ are the coordinates of any general point on the circle.
Substituting for ${{r}_{1}},g,f$, we get :
$\begin{align}
  & x=\dfrac{p}{\sqrt{2}}\cos t-\dfrac{p}{2} \\
 & y=\dfrac{p}{\sqrt{2}}\sin t-\dfrac{p}{2} \\
\end{align}$
Hence, this the parametric equation of the circle given to us.
So, answer is the parametric equation of the circle is : $\begin{align}
  & x=\dfrac{p}{\sqrt{2}}\cos t-\dfrac{p}{2} \\
 & y=\dfrac{p}{\sqrt{2}}\sin t-\dfrac{p}{2} \\
\end{align}$

Note: You should remember the general method of converting a general equation of a circle into the parametric equation form. The parametric equation of a circle can be directly written as : $\begin{align}
  & x=r\cos t+{{x}_{0}} \\
 & y=r\sin t+{{y}_{0}} \\
\end{align}$ where $({{x}_{0}},{{y}_{0}})$ is the centre of the circle and $r=$ the radius of the circle. This way, you can directly convert just by finding the centre and the radius of the given circle.