Question

Find the locus of a point equidistant from three collinear points.
A. A straight line
B. A pair of points
C. A point
D. The null set

Answer 1

Hint: Draw a line and place three collinear points in it. Then draw a perpendicular bisector between each of three points. Then obtain the locus of the points with the help of these perpendicular bisectors.

Complete step by step solution:
The diagram of the three equidistant point of a line with perpendicular bisector is,

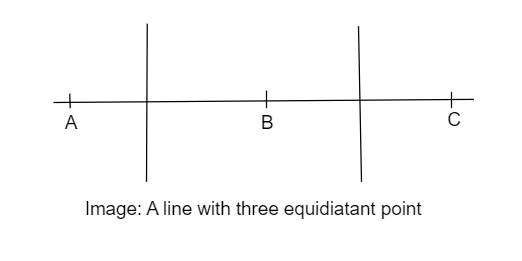
We know that a line through the point of intersection of the perpendicular bisector gives the locus of three equidistant collinear point, but from the diagram it is clear that there is no point of intersection of these two perpendicular bisectors as they are parallel lines.
Hence, the locus is a null set.

Option ‘D’ is correct

Additional information
In geometry, a locus is a collection of points that satisfy a particular requirement or circumstance for a shape or figure. The locus is pluralized as loci. The region is the space where the loci are located. Location is the ancestor of the word locus. Prior to the 20th century, geometric shapes were thought of as things or locations where points might be put or moved. However, in contemporary mathematics, the entities are seen as a collection of points that satisfy a particular condition.A locus is a curve or other shape created in mathematics from all the points that meet a specific equation describing the relationship between the coordinates, or from a point, line, or moving surface. The locus defines all shapes as a set of points, including circles, ellipses, parabolas, and hyperbolas.

Note: Sometimes students get into the calculation part and are unable to find the answer, so for this type of question draw a diagram and give the answer logically.