Question

Find the image of the point with the position vector \[i + 3k\] in the plane \[r \cdot \left( {i + j + k} \right) = 1\].
A. \[i + 2j + k\]
B. \[i + 2j - k\]
C. \[ - i - 2j + k\]
D. \[i - 2j + k\]

Answer 1

Hint: Assume that \[Q\] be the image of the point \[P\left( {i + 3k} \right)\]. Since the line \[PQ\] is perpendicular to plane \[r \cdot \left( {i + j + k} \right) = 1\], so the direction ratio of \[PQ\] will be \[i + j + k\]. By using the formula \[r = {r_0} + \lambda t\], we will find the equation of line \[PQ\]. Then we will find the midpoint of \[PQ\] and put it in the equation of the plane. After that, we will put the value of \[\lambda \] to get the vector \[Q\].

Formula used
The equation of the line is \[r = {r_0} + \lambda t\], where \[{r_0}\] is the point on the line and \[t\] is the direction ratio.
The midpoint of the points \[{x_1}i + {y_1}j + {z_1}k\] and \[{x_2}i + {y_2}j + {z_2}k\] is \[\dfrac{{\left( {{x_1} + {x_2}} \right)i + \left( {{y_1} + {y_2}} \right)j + \left( {{z_1} + {z_2}} \right)k}}{2}\].
The direction ratio of a line is equal to the direction ratio of the perpendicular plane of the line.
Dot product: \[\left( {{a_1}i + {b_1}j + {c_1}k} \right) \cdot \left( {{a_2}i + {b_2}j + {c_2}k} \right) = {a_1}{a_2} + {b_1}{b_2} + {c_1}{c_2}\]

Complete step by step solution

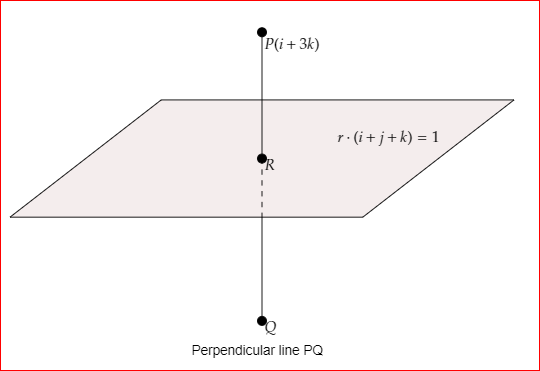
Image: Image of the point (i+3k).
Let \[Q\] be the image of the point \[P\left( {i + 3k} \right)\].
The direction ratio of a line is equal to the direction ratio of the perpendicular plane of the line.
Since \[PQ\] is perpendicular to the plane \[r \cdot \left( {i + j + k} \right) = 1\], the direction ratios of \[PQ\] are \[i + j + k\].
The line \[PQ\] passes through the point \[P\left( {i + 3k} \right)\].
Apply the formula \[r = {r_0} + \lambda t\] to find the equation of line \[PQ\].
\[r = i + 3k + \lambda \left( {i + j + k} \right)\]
\[ \Rightarrow r = \left( {1 + \lambda } \right)i + \lambda j + \left( {3 + \lambda } \right)k\]
Any point on line \[r = i + 3k + \lambda \left( {i + j + k} \right)\] will be \[\left( {1 + \lambda } \right)i + \lambda j + \left( {3 + \lambda } \right)k\].
Assume that the point of \[Q\] be \[\left( {1 + \lambda } \right)i + \lambda j + \left( {3 + \lambda } \right)k\].
Let \[R\] be the midpoint of the segment \[PQ\].
Apply the formula \[\dfrac{{\left( {{x_1} + {x_2}} \right)i + \left( {{y_1} + {y_2}} \right)j + \left( {{z_1} + {z_2}} \right)k}}{2}\] to get the midpoint of \[PQ\].
Here \[{x_1}i + {y_1}j + {z_1}k = i + 3k\] and \[{x_2}i + {y_2}j + {z_2}k = \left( {1 + \lambda } \right)i + \lambda j + \left( {3 + \lambda } \right)k\]
The midpoint of \[PQ\] is \[\dfrac{{1 + 1 + \lambda }}{2}i + \dfrac{\lambda }{2}j + \dfrac{{3 + 3 + \lambda }}{2}k\]
                                        \[ = \dfrac{{2 + \lambda }}{2}i + \dfrac{\lambda }{2}j + \dfrac{{6 + \lambda }}{2}k\]
Since the midpoint lies on the plane \[r \cdot \left( {i + j + k} \right) = 1\], so \[R\] will satisfy the plane.
\[\left( {\dfrac{{2 + \lambda }}{2}i + \dfrac{\lambda }{2}j + \dfrac{{6 + \lambda }}{2}k} \right) \cdot \left( {i + j + k} \right) = 1\]
Apply the dot product on the left side \[\left( {{a_1}i + {b_1}j + {c_1}k} \right) \cdot \left( {{a_2}i + {b_2}j + {c_2}k} \right) = {a_1}{a_2} + {b_1}{b_2} + {c_1}{c_2}\]
\[ \Rightarrow \dfrac{{2 + \lambda }}{2} \cdot 1 + \dfrac{\lambda }{2} \cdot 1 + \dfrac{{6 + \lambda }}{2} \cdot 1 = 1\]
\[ \Rightarrow \dfrac{{2 + \lambda }}{2} + \dfrac{\lambda }{2} + \dfrac{{6 + \lambda }}{2} = 1\]
Calculate the value of \[\lambda \] from the above equation
\[ \Rightarrow 2 + \lambda + \lambda + 6 + \lambda = 2\]
\[ \Rightarrow 3\lambda + 8 = 2\]
\[ \Rightarrow 3\lambda = - 6\]
\[ \Rightarrow \lambda = - 2\]
Now putting \[\lambda = - 2\] in \[\left( {1 + \lambda } \right)i + \lambda j + \left( {3 + \lambda } \right)k\]
\[\left( {1 + \lambda } \right)i + \lambda j + \left( {3 + \lambda } \right)k = \left( {1 - 2} \right)i + \left( { - 2} \right)j + \left( {3 - 2} \right)k\]
\[ = - i - 2j + k\]
Thus, the image of the point \[i + 3k\] is \[ - i - 2j + k\].

Note: Many students make a mistake to take the image point. They take \[R\] as the image on the plane. The distance of the point \[P\] from the plane is the same as the distance of the image point \[P\] from the plane.