Question

Find the equation of circle passing through (-1, -3) & touching 4x + 3y – 12 = 0 at (3, 0).

Answer 1

Hint: To find the equation of a circle, we need to find the center of the circle and compare the radius of the circle.

Formula Used: 1) \[\begin{array}{*{20}{c}}
  d& = &{\sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}} }
\end{array}\]
2) \[\begin{array}{*{20}{c}}
  {{m_1} \times {m_2}}& = &{ - 1}
\end{array}\]
3) \[\begin{array}{*{20}{c}}
  m& = &{\dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}}
\end{array}\]

Complete step by step solution: Let us assume that the coordinates of the center of the circle (h, k) and the radius of the circle is r. We have given that the circle is passing through the point (-1, -3) and touching the line 4x + 3y -12 = 0.
Now we will draw a figure according to the given conditions,

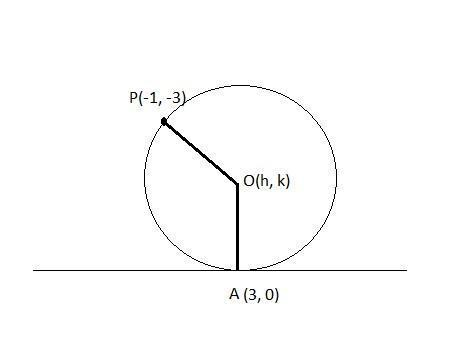
Figure 1

Now, according to the figure, we can conclude that the length of the Po and OA will be equal. Therefore, we can write that
\[\begin{array}{*{20}{c}}
  { \Rightarrow PO}& = &{OA}
\end{array}\]
Now we know that
\[\begin{array}{*{20}{c}}
  { \Rightarrow d}& = &{\sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}} }
\end{array}\]
Therefore, we will
\[\begin{array}{*{20}{c}}
  { \Rightarrow \sqrt {{{(h + 1)}^2} + {{(k + 3)}^2}} }& = &{\sqrt {{{(3 - h)}^2} + {{(0 - k)}^2}} }
\end{array}\]
Now, square both the side, we will get
\[\begin{array}{*{20}{c}}
  { \Rightarrow {{(h + 1)}^2} + {{(k + 3)}^2}}& = &{{{(3 + h)}^2} + {{(0 - k)}^2}}
\end{array}\]
\[\begin{array}{*{20}{c}}
  { \Rightarrow 8h + 6k}& = &{ - 1}
\end{array}\] ……………. (a)
Now we will determine the slope of the line 4x + 3y -12 = 0,
\[\begin{array}{*{20}{c}}
  { \Rightarrow 4x + 3y - 12}& = &0
\end{array}\]
\[\begin{array}{*{20}{c}}
  { \Rightarrow m}& = &{ - \dfrac{a}{b}}
\end{array}\]
\[\begin{array}{*{20}{c}}
  { \Rightarrow m}& = &{ - \dfrac{4}{3}}
\end{array}\]
This is the slope of the line 4x + 3y -12 = 0. So the slope of the line AO will be,
\[\begin{array}{*{20}{c}}
  { \Rightarrow m \times {m_{AO}}}& = &{ - 1}
\end{array}\]
Therefore,
\[\begin{array}{*{20}{c}}
  { \Rightarrow - \dfrac{4}{3} \times {m_{AO}}}& = &{ - 1}
\end{array}\]
\[\begin{array}{*{20}{c}}
  { \Rightarrow {m_{AO}}}& = &{\dfrac{3}{4}}
\end{array}\]
Therefore, we know that
\[\begin{array}{*{20}{c}}
  { \Rightarrow m}& = &{\dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}}
\end{array}\]
Therefore, for the two points A and O,
\[\begin{array}{*{20}{c}}
  { \Rightarrow \dfrac{3}{4}}& = &{\dfrac{{k - 0}}{{h - 3}}}
\end{array}\]
\[\begin{array}{*{20}{c}}
  { \Rightarrow 3h - 4k}& = &9
\end{array}\] ………….. (b)
From the equation (a) and (b), we will get
\[\begin{array}{*{20}{c}}
  { \Rightarrow h}& = &1
\end{array}\] and
 \[\begin{array}{*{20}{c}}
  { \Rightarrow k}& = &{ - \dfrac{3}{2}}
\end{array}\].
Therefore, the center of the circle is \[\left( {1, - \dfrac{3}{2}} \right)\].
And we will find the radius of the circle that is AO and PO. Therefore,
\[\begin{array}{*{20}{c}}
  { \Rightarrow r}& = &{\sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}} }
\end{array}\]
For the coordinates A and O,
\[\begin{array}{*{20}{c}}
  { \Rightarrow r}& = &{\sqrt {{{(3 - 1)}^2} + {{\left( {0 + \dfrac{3}{2}} \right)}^2}} }
\end{array}\]
\[\begin{array}{*{20}{c}}
  { \Rightarrow r}& = &{\dfrac{5}{2}}
\end{array}\]
Now, we know the general equation of the circle having the coordinates and the radius.
\[\begin{array}{*{20}{c}}
  { \Rightarrow {{(x - h)}^2} + {{(y - k)}^2}}& = &{{r^2}}
\end{array}\]
Now we have the center of the circle and the radius of the circle, therefore we will put the value in the above equation,
\[\begin{array}{*{20}{c}}
  { \Rightarrow {{(x - 1)}^2} + {{\left( {y + \dfrac{3}{2}} \right)}^2}}& = &{{{\left( {\dfrac{5}{2}} \right)}^2}}
\end{array}\]
\[\begin{array}{*{20}{c}}
  { \Rightarrow {x^2} + {y^2} - 2x + 3y - 3}& = &0
\end{array}\]

So the equation of the circle is $ {x^2} + {y^2} - 2x + 3y - 3 = 0$.

Note: It is important to note that the length of the line AO and the length of the line PO will be equal. The length of the line AO and PO are also called the radius of the circle.