Question

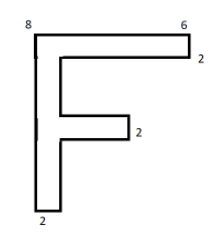
Find the centre of mass of the given letter $F$ which is cut from a uniform metal sheet.

A) $\dfrac{{15}}{7},\dfrac{{23}}{7}$
B) $\dfrac{{33}}{7},\dfrac{{15}}{7}$
C) $\dfrac{{22}}{7},\dfrac{{33}}{7}$
D) $\dfrac{{33}}{7},\dfrac{{22}}{7}$

Answer 1

Hint: The centre of mass of a mass distribution in space is the single point at which the weighted relative location of the distributed mass sums is at zero. This is where a force can be used to induce a linear acceleration without an acceleration of the angle. Calculations of the mechanics of the centre of mass are also generalised. The whole mass of an object may be believed to be condensed to imagine the motion of that object. This means that in a single object with the application of Newton's laws of motion, the centre of mass is a particle relative.
If one body is rigid, the centre of weight is fastened to the body. In case of a single rigid body, the centre of mass is positioned in the centre. As in some situations with hollow or open-shaped objects, such as a horseshoe, the centre of weight may be found outside the corporal.

Complete step by step solution:
The figure is divided into three parts,
Considering the mass per area of sheet to be $k$.
$k = \dfrac{m}{A}$
$ \Rightarrow m = k \times A$
Using the formula of centre of mass,
Centre of mass along $x$ axis
${X_ {cm}} = \dfrac{{{m_1}{x_1} + {m_2} {x_2} + {m_3} {x_3}}} {{{m_1} + {m_2} + {m_3}}} $
$ \Rightarrow {X_ {cm}} = \dfrac{{k \times 6 \times 2 \times 3 + k \times 2 \times 6 \times 1 + k \times 2 \times 2 \times 3}} {{k \times 6 \times 2 + k \times 2 \times 6 + k \times 2 \times 2}}$
$ \Rightarrow {X_ {cm}} = \dfrac{{15}}{7}$
Centre of mass along $y$ axis
${Y_ {cm}} = \dfrac{{{m_1}{y_1} + {m_2} {y_2} + {m_3} {y_3}}} {{{m_1} + {m_2} + {m_3}}} $
$ \Rightarrow {Y_ {cm}} = \dfrac{{k \times 6 \times 2 \times 1 + k \times 2 \times 6 \times 5 + k \times 2 \times 2 \times 5}} {{k \times 6 \times 2 + k \times 2 \times 6 + k \times 2 \times 2}} $
$ \Rightarrow {Y_ {cm}} = \dfrac{{23}}{7}$

Correct option is (A).

Note: When different bodies such as planets in the solar system are dispersed, the mass centre may not fit the location of each individual system member. The centre of mass is a valuable point of reference for measurements in the area of mechanical applications concerning space masses, such as the linear and angular momentum and rigid body mechanics of celestial bodies. The calculations of the motion of planets was formulated in orbital mechanics as point masses at the centres of the mass. The core of the mass frame is an inertial structure in which the mass core of the system lies with reference to its origin.