Question

Find out the expression for the torque acting on a coil having an area of cross-section, $A$ , number of turns $n$ , placed in a magnetic field of intensity $B$ , making an angle $\theta $ with the normal of the coil, when a current $i$ is flowing it.
A. $niAB\tan \theta $
B. $niAB\cos \theta $
C. $niAB\sin \theta $
D. $niAB$

Answer 1

Hint:The above question is asking you to derive the formula for the torque that a current carrying coil experiences when it is placed in a magnetic field. Consider a rectangular loop and calculate the net torque it experiences, when the axis of the loop is placed at an angle to the magnetic field.




Complete answer:
Consider a rectangular loop of sides $a$ and $b$ , carrying current $i$ , placed in a uniform magnetic field of intensity $B$ .
Each side of the loop will act like a current carrying wire in a magnetic field and hence, will experience force equivalent to $iBa\sin ({90^ \circ })$ or $iBb\sin ({90^ \circ })$ depending on the length of the wire.
Let the loop be placed in such a way that the area vector (normal to the area of the loop), is along the direction of the magnetic field.


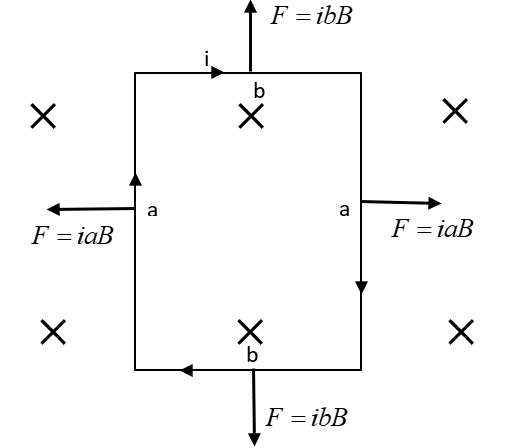
In this case, the net force on the loop will be 0 and the net torque on the loop will be 0 as well as they all cancel each other.
Now, let us rotate the coil by some angle $\theta $ .

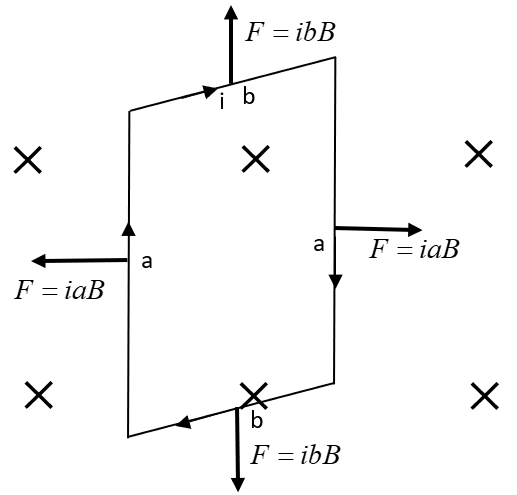
In this case the net force on the loop will still be 0. However, the torque is not. Hence, the current carrying loop experienced a torque when placed in a magnetic field.
The vertical forces cancel each other but the horizontal forces did not as they are not having the same line of action.
As, both the horizontal forces are rotating the loop in the same direction, therefore,
${\tau _{{\text{net}}}} = F \times \left( {{\text{the perpendicular distance}}} \right) + F \times \left( {{\text{the perpendicular distance}}} \right)$

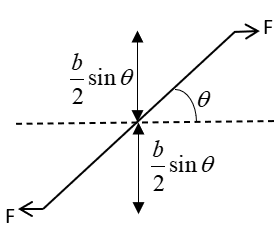
This perpendicular distance is equivalent to $\dfrac{b}{2}\sin \theta $ as seen in the figure.
Hence, ${\tau _{{\text{net}}}} = 2F \times \dfrac{b}{2}\sin \theta = Fb\sin \theta $ .
Now, this force $F$ is equal to $iBa\sin ({90^ \circ }) = iBa$ as said above.
Hence, substituting this, we get:
${\tau _{{\text{net}}}} = (iBa)(b\sin \theta )$
As area of the loop, $A = ab$ ,
${\tau _{{\text{net}}}} = iAB\sin \theta $
Considering there are $n$ number of turns in the coil, the net torque on the coil will be:
${\tau _{{\text{net}}}} = niAB\sin \theta $
Hence, the correct option is C.




Note:Torque is a force that rotates a body, that is, it is a rotational equivalent of force. In the above derivation, it is important to consider how the forces cancel out each other in both the cases but the torque does not. It is because only the vertical forces cancelled each other but the horizontal forces did not. This happened because the line of action of these horizontal forces were different. If they were along the same line (the first case), they would have cancelled each other as well and the net torque would have been 0.