
How many electrons should be removed from a coin of mass $1.6g$, so that it may float in an electric field of intensity ${10^9}N{C^{ - 1}}$ directed upward?
A) $9.8 \times {10^7}$
B) $9.8 \times {10^5}$
C) $9.8 \times {10^3}$
D) $9.8 \times {10^1}$
Answer
217.8k+ views
Hint: In the question, it’s given that the coin is floating. The coin will float only when the net force is zero or the forces are balanced i.e. the force due to the electric field is equal to the weight of the electron. From this, we can easily calculate the charge required to balance the electron and from that, we can calculate the amount of electron which will be removed.
Formulae used:
${N_e} = \dfrac{q}{{{C_e}}}$
Here ${N_e}$ is the number of electrons, $q$ is the total charge and ${C_e}$ is the charge on one electron.
Complete step by step answer:
In the question, a coin of mass $1.6g$ is given. It is said that it is floating in the electric field of $109N{C^{ - 1}}$.
Let us draw the free body diagram of the coin.
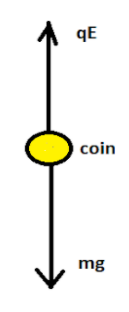
For the coin to float it should be in a balanced condition. The upward force acting on the coin should be equal to the downward force acting on the body. Hence
$ \Rightarrow qE = mg$
Where $q$ is the net charge on the coin, $E$ is the electric field acting on the body, $m$ is the mass of the coin and $g$ is the acceleration due to gravity.
Let this be equation 1.
It’s given that,
$m = 1.6g = 1.6 \times {10^{ - 3}}kg$
$E = {10^9}N{C^{ - 1}}$
$g = 9.8m{s^{ - 2}}$
Putting the values of $m$, $E$ and $g$ in the equation 1, we get,
$ \Rightarrow q \times 109 = 1.6 \times {10^{ - 3}} \times 9.8$
$ \therefore q = \dfrac{{1.6 \times {{10}^{ - 3}} \times 9.8}}{{{{10}^9}}}$
We know that the charge on one electron is $1.6 \times {10^{ - 19}}C$.
The number of electrons that is required to be removed,
$ \Rightarrow {N_e} = \dfrac{q}{{{C_e}}}$
Here ${N_e}$ is the number of electrons, $q$ is the total charge and ${C_e}$ is the charge on one electron.
$ \Rightarrow {N_e} = \dfrac{q}{{{C_e}}}$
$ \therefore {N_e} = \dfrac{{\dfrac{{1.6 \times {{10}^{ - 3}} \times 9.8}}{{{{10}^9}}}}}{{1.6 \times {{10}^{ - 19}}C}} = 9.8 \times {10^7}$
So option (A) is the correct answer.
Note: Any charge when placed in an external electric field will experience an electric force. In this case the force experienced by all the electrons in the coin should balance the weight of the coin. We will not consider the electric force acting on the protons because this electric force acting on them is negligible as compared to the intranuclear forces inside the nucleus of the atoms. So, only the force on the electrons is considered.
Formulae used:
${N_e} = \dfrac{q}{{{C_e}}}$
Here ${N_e}$ is the number of electrons, $q$ is the total charge and ${C_e}$ is the charge on one electron.
Complete step by step answer:
In the question, a coin of mass $1.6g$ is given. It is said that it is floating in the electric field of $109N{C^{ - 1}}$.
Let us draw the free body diagram of the coin.

For the coin to float it should be in a balanced condition. The upward force acting on the coin should be equal to the downward force acting on the body. Hence
$ \Rightarrow qE = mg$
Where $q$ is the net charge on the coin, $E$ is the electric field acting on the body, $m$ is the mass of the coin and $g$ is the acceleration due to gravity.
Let this be equation 1.
It’s given that,
$m = 1.6g = 1.6 \times {10^{ - 3}}kg$
$E = {10^9}N{C^{ - 1}}$
$g = 9.8m{s^{ - 2}}$
Putting the values of $m$, $E$ and $g$ in the equation 1, we get,
$ \Rightarrow q \times 109 = 1.6 \times {10^{ - 3}} \times 9.8$
$ \therefore q = \dfrac{{1.6 \times {{10}^{ - 3}} \times 9.8}}{{{{10}^9}}}$
We know that the charge on one electron is $1.6 \times {10^{ - 19}}C$.
The number of electrons that is required to be removed,
$ \Rightarrow {N_e} = \dfrac{q}{{{C_e}}}$
Here ${N_e}$ is the number of electrons, $q$ is the total charge and ${C_e}$ is the charge on one electron.
$ \Rightarrow {N_e} = \dfrac{q}{{{C_e}}}$
$ \therefore {N_e} = \dfrac{{\dfrac{{1.6 \times {{10}^{ - 3}} \times 9.8}}{{{{10}^9}}}}}{{1.6 \times {{10}^{ - 19}}C}} = 9.8 \times {10^7}$
So option (A) is the correct answer.
Note: Any charge when placed in an external electric field will experience an electric force. In this case the force experienced by all the electrons in the coin should balance the weight of the coin. We will not consider the electric force acting on the protons because this electric force acting on them is negligible as compared to the intranuclear forces inside the nucleus of the atoms. So, only the force on the electrons is considered.
Recently Updated Pages
Charge in a Magnetic Field: Definition, Formula & Examples

Charging and Discharging of a Capacitor Explained Simply

Combination of Capacitors: Series and Parallel Explained

Compressibility Factor Explained: Definition, Formula & Uses

Compressibility Factor Z: Definition, Formula & Uses

Conduction Band Explained: Definition, Importance & Examples

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

Understanding Collisions: Types and Examples for Students

How to Convert a Galvanometer into an Ammeter or Voltmeter

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Understanding Atomic Structure for Beginners

Ideal and Non-Ideal Solutions Explained for Class 12 Chemistry

Degree of Dissociation: Meaning, Formula, Calculation & Uses

Understanding Electromagnetic Waves and Their Importance

Understanding the Electric Field of a Uniformly Charged Ring




