Question

Consider the circuit shown in the figure

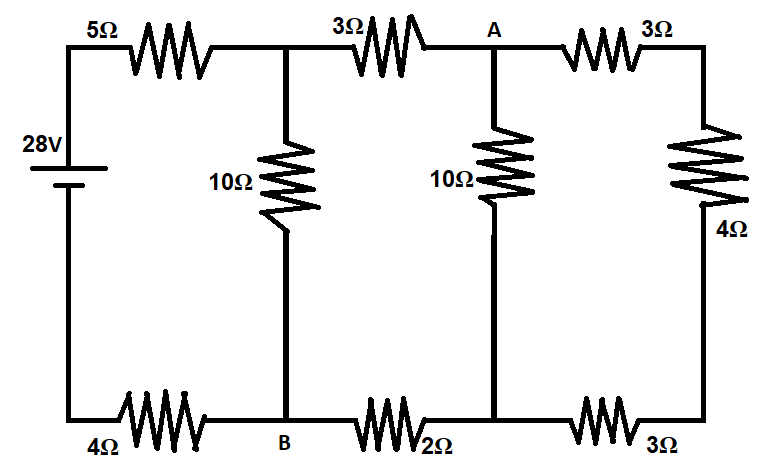
A) The current in the $5\Omega $ resistor is $2A$.
B) The current in the $5\Omega $ resistor is $1A$.
C) The potential difference ${V_A} - {V_B}$ is $10V$.
D) The potential difference ${V_A} - {V_B}$ is $5V$.

Answer 1

Hint:To find the current through the voltage source, we have to evaluate resistance and apply Ohm's law. Calculate the equivalent resistance from the rightmost resistors and evaluate the voltage. Then use Kirchhoff's law to evaluate the potential. According to Kirchhoff's law, the algebraic sum of all currents entering a junction will be equal to the algebraic sum leaving the junction.

Formula used:
i) In series, $R = {R_1} + {R_2} + .......{R_n}$ (where R is the equivalent resistance, ${R_1},{R_2}......{R_n}$ stands for the individual resistances in the circuit)
ii) In parallel, \[\dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + .....\dfrac{1}{{{R_n}}}\] (where R is the equivalent resistance, ${R_1},{R_2}......{R_n}$ stands for the individual resistances in the circuit)
iii) The current using Ohm’s law is given by, $I = \dfrac{V}{R}$ (Where I is the current through the circuit, V is the potential difference and R is the total resistance of the circuit)

Complete step by step solution:
Let us consider the circuit from the point marked A.

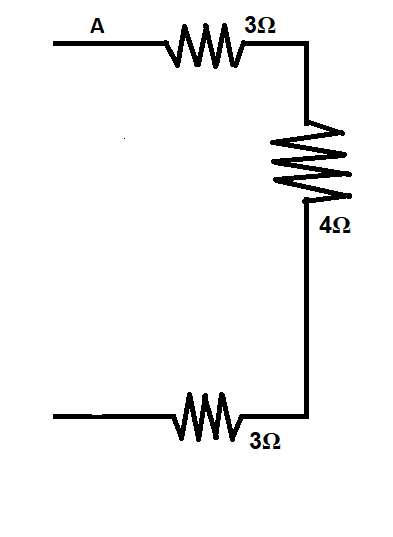
The three resistors $3\Omega, 4\Omega$ & $3\Omega$ are connected in series, therefore their equivalent resistance can be written as,
Resistance equivalent of $3\Omega, 4\Omega$ & $3\Omega $ $ = 3 + 4 + 3 = 10\Omega $
Now let us replace the three resistors in series with their equivalent resistance and consider the next part of the circuit

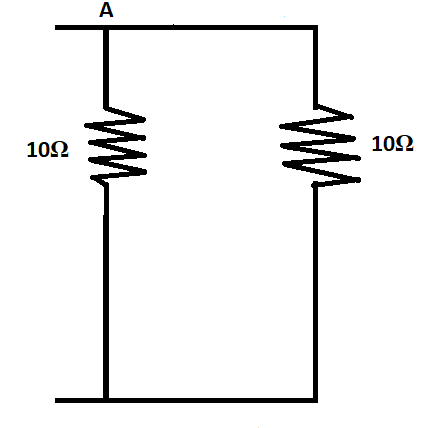
Now the two resistors are in parallel, their equivalent resistance can be calculated in the following steps.
Effective resistance, $\dfrac{1}{R} = \dfrac{1}{{10}} + \dfrac{1}{{10}} = 0.2\Omega $
The equivalent resistance, $R = \dfrac{1}{{0.2}} = 5\Omega $
Now we can replace the two resistance with their equivalent resistance in the circuit,

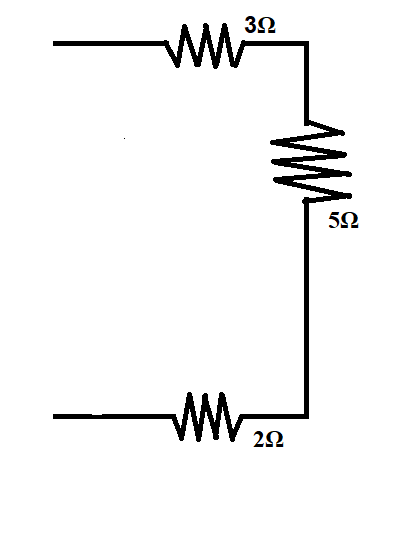
Now, these three resistances are in series, their equivalent resistance can be calculated as,
Resistance equivalent $3\Omega, {\text{ }}5\Omega {\text{ }}\& {\text{ }}2\Omega = 3 + 5 + 2 = 10\Omega $
Now these three resistors can be replaced by their equivalent resistance

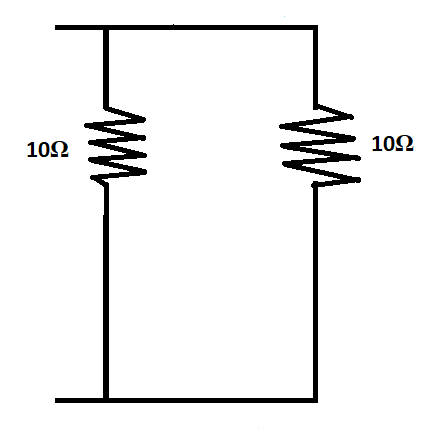
These two resistors are in parallel connection, hence their equivalent resistance is given by,
Effective resistance, $\dfrac{1}{R} = \dfrac{1}{{10}} + \dfrac{1}{{10}} = 0.2\Omega $
The equivalent resistance, $R = \dfrac{1}{{0.2}} = 5\Omega $
Replacing these two resistors in the circuit,

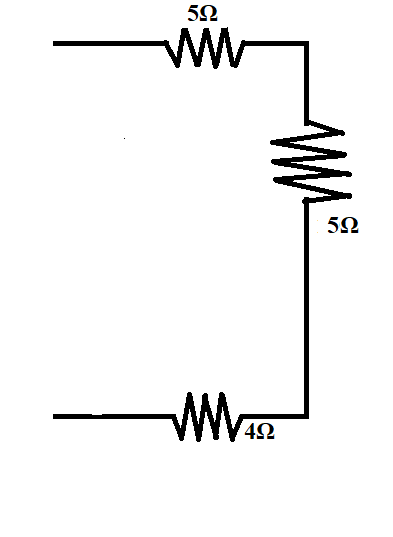
Now the effective resistance of these three resistors will be the total equivalent resistance of the entire circuit.
Since the three resistors are in series,
The equivalent resistance of the circuit, $R = 5\Omega + 5\Omega + 4\Omega = 14\Omega $
The Potential difference is $28 V$(given in the question)
Current through the source can be obtained by applying Ohm’s law
$I = \dfrac{V}{R}A$
Given that $V = 28 Volt$ and $R = 14\Omega $ (R is calculated through the above steps)
The current through the source, $I = \dfrac{V}{R}A$
$I = \dfrac{{28}}{{14}}A$$ = 2 A$
$\therefore $The current through $5\Omega $ resistance = $2 A$

To find the current through each branch, we have to go through the simplified circuit in the reverse order.


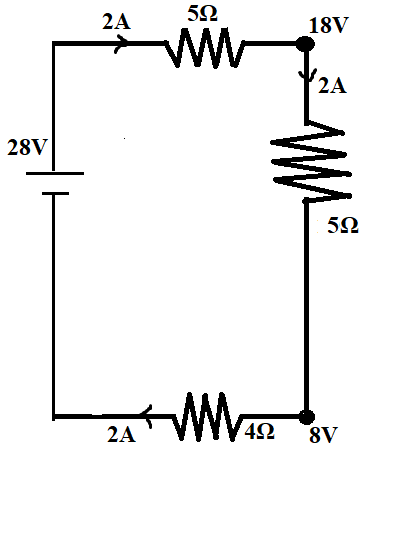
The current through $5\Omega $ resistance =$2 A$, (since there is no other resistance before $5\Omega $ resistor)
The current through the next $3\Omega$ resistor can be calculated using the next diagram

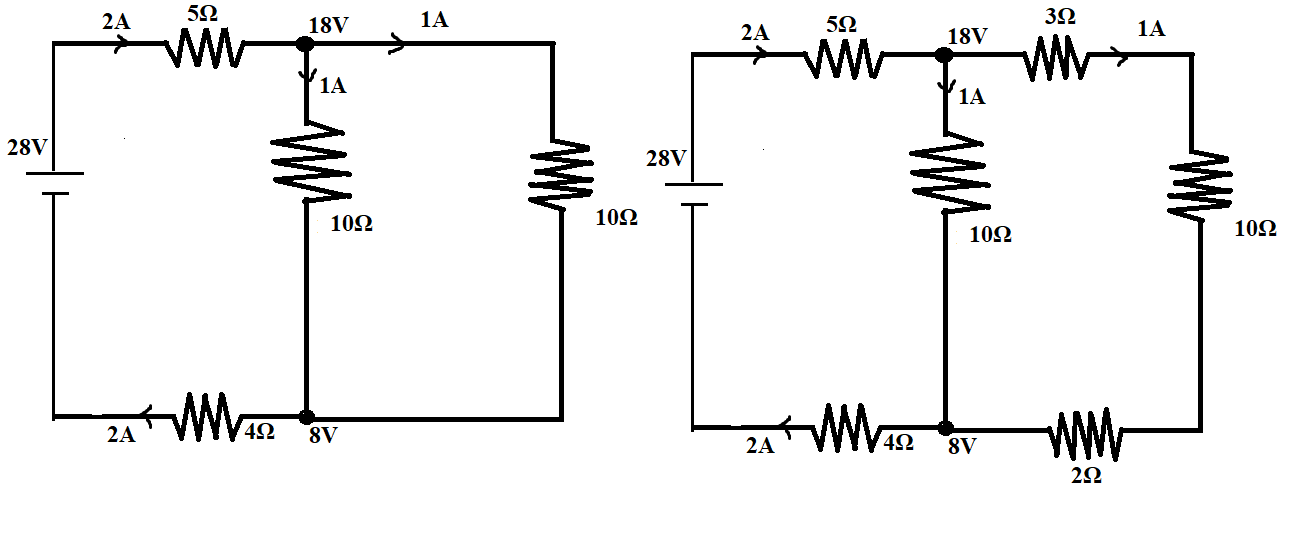
The $2A$ current will split into two, since the two branches have the same equivalent resistance the current will be split into half.
The current through the next $3\Omega$ resistor will be= $\dfrac{{2A}}{2} = 1A$
In the same way, the current through the next $3\Omega $ resistor can be calculated

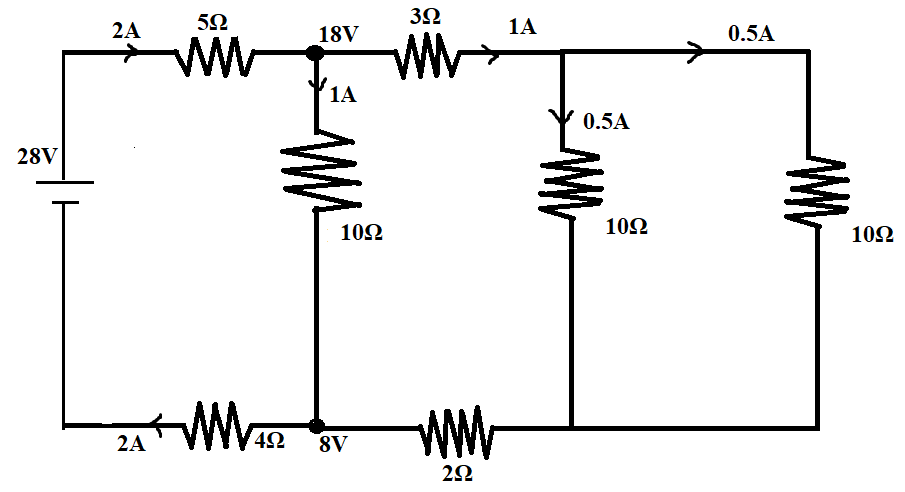
There are again two branches with equal resistance, the current will again split into half,
The current through the next $3\Omega $ resistor = $\dfrac{{1A}}{2} = 0.5A$
$\therefore $The current through $5\Omega $ resistance = $2A$
The current through the next $3\Omega $resistor = $1A$
The current through the next $3\Omega $ resistor = $0.5A$
Applying Kirchhoff’s law from A to B,
${V_A} - (3 + 4 + 3)0.5 - 2 \times (1) - {V_B} = 0$
From the above equation, we get
${V_A} - {V_B} = 7V$

The correct answer is (A), The current in the $5\Omega $ resistor is $2A$.

Note:To find the equivalent resistance of several resistors that are connected in series we take the individual sum of resistances. In a series combination, the equivalent resistance will be higher than the value of the highest resistance in the circuit. On the other hand, in parallel combination, the effective resistance will be less than the lowest value of resistance in the circuit.