Question

Cell constant of a conductivity cell is:
(A) $\text{Specific conductance / Resistance}$
(B) $\text{Specific conductance }\times \dfrac{1000}{Normality}$
(C) $\text{Specific conductance / Conductance}$
(D) $\text{Conductance / Specific conductance}$

Answer 1

Hint: Cell constant of a cell can be derived from both resistance and conductance. The right answer in this case includes specific conductance and conductance.

Complete step-by-step answer:
Let’s start with understanding the concept of cell constant. You must already know from your lessons in physics that resistance of a material is related to its length, area of cross-section and nature. Same theory applies to chemical solutions. But it has some differences. Such as how would you define the length and area of the cross section of a solution?
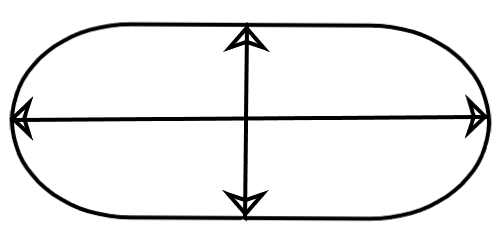
To overcome these problems, these ionic solutions are taken inside things known as conductivity cells (as represented below). These are actually tubular structures with the horizontal line referring to its length and the vertical line as its area of cross section. Now the calculations become easier.

The resistance (R) is equal to:
\[R=\rho \dfrac{L}{A}\]
Where “$\rho $ ” is known as specific resistance or resistivity, “$L$” is the length and “$A$” is the area of cross-section of the resistor. As for an ionic solution, its length and area of cross section depend on the dimensions of the conductivity cells, they are taken as a constant for a specific experiment. This constant is termed as cell constant and represented as $G*$.
\[G*=\dfrac{L}{A}\]
This makes the equation of resistance as:
\[R=\rho \dfrac{L}{A}=\rho \operatorname{G}*\]
And therefore cell constant is also equal to:
\[G*=\dfrac{R}{\rho }\]
That is, cell constant is the ratio between resistance and specific resistance or resistivity. But the options do not include this.
Let us take this chance to define conductance. As its name suggests, it is opposite to that of resistance and is mathematically the reciprocal of resistance. It is represented as $G$.
\[G=\dfrac{1}{R}=\dfrac{A}{\rho L}\]
The quantity “$1/\rho $” is known as specific conductance or conductivity. So the above equation becomes:
\[G=\dfrac{\kappa A}{L}\]
And as cell constant is the ratio of length and area, we can get another expression by rearranging the above equation, as:
\[\begin{align}
  & G=\dfrac{\kappa A}{L}=\dfrac{\kappa }{L/A} \\
 & \Rightarrow G=\dfrac{\kappa }{\operatorname{G}*} \\
\end{align}\]
Now the cell constant has a new definition. It can be defined as the ratio between specific conductance or conductivity and conductance, as:
\[\operatorname{G}*=\dfrac{\kappa }{G}\]
Therefore the answer is option (C) $\text{Specific conductance / Conductance}$.

Note: The IUPAC has recommended the use of resistivity in place of specific resistance and conductivity in place of specific conductance. But these terms are still interchanged in some places.
Cell constant is an important parameter in defining molar conductivity of diluted solutions.
$G$ and $\operatorname{G}*$ both represent two different quantities. The former is conductance while the latter is the cell constant.