Question

When the bob of a pendulum is at the mean position (minimum displacement) of its motion, its total energy is
(A) All potential
(B) Zero
(C) All kinetic
(D) Partly kinetic partly potential

Answer 1

Hint A pendulum possesses both the kinetic energy and the potential energy when it is undergoing oscillations about its mean position. The variation of one energy is inverse to the variation of the other energy such that the total energy remains conserved.

Complete Step by step solution
Kinetic energy is defined as the energy possessed by an object by the virtue of its motion while potential energy is the energy possessed by an object by the virtue of its position. When a pendulum undergoes oscillatory motion about its mean position then it possesses both the kinetic energy and the potential energy.
The kinetic energy of the bob of the pendulum is zero at the extreme positions while its value is maximum when it passes through its mean position.
The behaviour of the potential energy is opposite to that of the kinetic energy. The potential energy of the bob of the pendulum is maximum at the extreme positions and zero when it passes through its mean position.
The following graph shows the variation of the kinetic energy and the potential energy of a pendulum oscillating about its mean position.

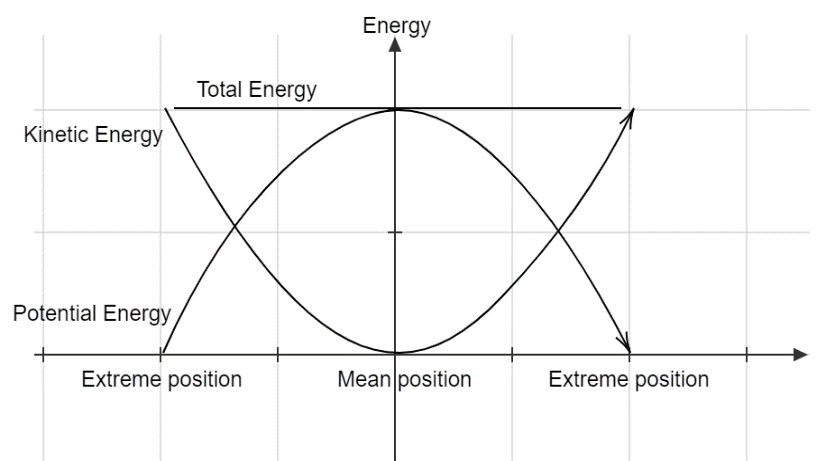
The total energy of the pendulum is equal to the sum of the kinetic energy and potential energy and its value remains constant throughout the motion of the pendulum.

Based on the above discussion we say that the correct answer is option (C) All kinetic.

Note The opposite variation of the kinetic energy and the potential energy ensures that the total energy of the pendulum remains constant. When the pendulum is at its extreme position, it momentarily comes to rest due to which the kinetic energy becomes zero at the extreme positions.