Question

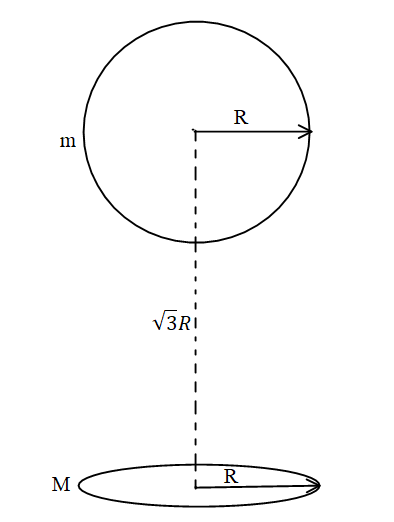
A uniform ring of mass M is lying at a distance $\sqrt 3 R$ from the centre of a uniform sphere of mass m just below the sphere as shown in the figure where R is the radius of the ring as well as that of the sphere. The gravitational force exerted by the ring on the sphere is:

Answer 1

Hint: The gravitational force is defined as the force of attraction or repulsion that acts between two bodies of similar or different masses. The acceleration due to gravity is also the result between the force acting between mass of an object and earth.

Formula used: The formula of the gravitational force between two masses is given by,
$F = \dfrac{{G{m_1}{m_2}}}{{{r^2}}}$
Where G is the universal gravitational constant ${m_1}$ and ${m_2}$ are the masses of the two bodies and r is the distance between the bodies.

Complete step by step solution:
Let a small element dM on the ring and sphere of mass m and calculate the force of gravitation on the sphere due to the ring.


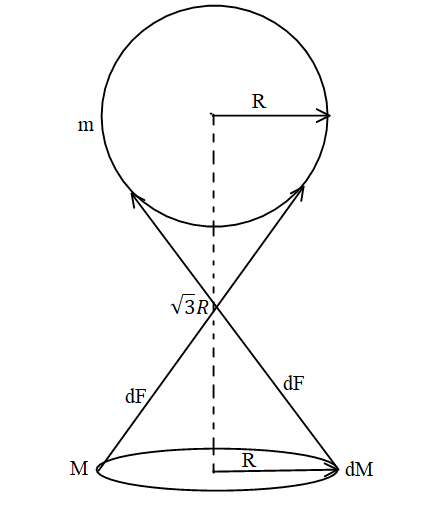
Angle $\theta $ is between the force dF and the vertical line joining the centre of the ring and the sphere.
The angle $\theta $ can be calculated as follows,
\[ \Rightarrow \tan \theta = \dfrac{R}{{R\sqrt 3 }}\]
\[ \Rightarrow \tan \theta = \dfrac{1}{{\sqrt 3 }}\]
\[ \Rightarrow \theta = {\tan ^{ - 1}}\dfrac{1}{{\sqrt 3 }}\]
\[ \Rightarrow \theta = 30^\circ \].
The force in the x-direction will be cancelled out but the force in the y-direction remains.
The force due to dM is given by,
$ \Rightarrow dF = \dfrac{{Gm\left( {dM} \right)}}{{{{\left( {\sqrt {{{\left( {R\sqrt 3 } \right)}^2} + {R^2}} } \right)}^2}}}$
$ \Rightarrow dF = \dfrac{{Gm\left( {dM} \right)}}{{{{\left( {\sqrt {4{R^2}} } \right)}^2}}}$
$ \Rightarrow dF = \dfrac{{Gm\left( {dM} \right)}}{{4{R^2}}}$
Taking force in the y-direction we get,
$ \Rightarrow d{F_y} = \dfrac{{Gm\left( {dM} \right)}}{{4{R^2}}}\cos 30^\circ $
As the value of $\cos 30^\circ $ is equal to$\dfrac{{\sqrt 3 }}{2}$.
$ \Rightarrow d{F_y} = \dfrac{{Gm\left( {dM} \right)}}{{8{R^2}}} \times \sqrt 3 $
$ \Rightarrow d{F_y} = \dfrac{{Gm\left( {dM} \right)}}{{8{R^2}}} \times \sqrt 3 $
Now let us calculate the total force on the sphere due to the ring, integrate the value of the force due to the small element of mass dM of the ring,
$\int\limits_{dM} {dF} = \int\limits_{dM} {\dfrac{{\sqrt {3 \cdot } Gm\left( {dM} \right)}}{{8{R^2}}}} $
After integrating we get,
$F = \dfrac{{\sqrt {3 \cdot } G \cdot M \cdot m}}{{8{R^2}}}$

The gravitational force on the sphere by the ring is equal to $F = \dfrac{{\sqrt {3 \cdot } G \cdot M \cdot m}}{{8{R^2}}}$.

Note: There is force of attraction or repulsion between everybody present on earth or outside the earth. If a body possesses mass then it feels force due to gravitation. The gravitational force is always attractive irrespective of the mass and the distance between.