Question

A trolley of mass $60\,kg$ moves on a smooth horizontal surface and has kinetic energy $120\,J$. A mass of $40\,kg$ is lowered vertically onto the trolley. The total kinetic energy of the system after lowering the mass is:
A) $60\,J$
B) $72\,J$
C) $120\,J$
D) $144\,J$

Answer 1

Hint: The kinetic energy depends upon mass and velocity of the body. The total mass will be the sum of mass of the trolley and the mass that is lowered onto the trolley. To find the velocity of the trolley after lowering the mass we can use the conservation of momentum. According to conservation of momentum the initial momentum will be equal to the final momentum.

Complete step by step solution:
It is given that a trolley has a mass, ${m_1} = 60\,kg$ .
The kinetic energy of the trolley is
$KE = 120\,J$ .

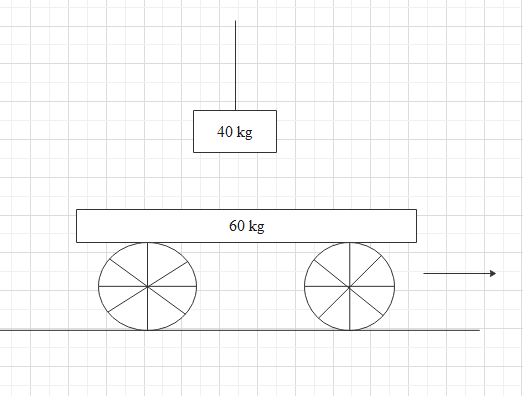
We need to find the kinetic energy when a mass of $40\,kg$ is lowered vertically onto the trolley.
The kinetic energy is the energy possessed by a body by virtue of its motion. Kinetic energy can be calculated as
$KE = \dfrac{1}{2}m{v^2}$
Where, m is the mass, v is the velocity.
By substituting the given values in the equation, we can find the value of initial velocity, ${v_i}$ as
$ \Rightarrow 120 = \dfrac{1}{2} \times 60 \times {v_i}^2$
$ \Rightarrow {v_i} = 2\,\,m/s$
In order to find the final velocity after lowering the mass onto the trolley we can use the law of conservation of momentum.

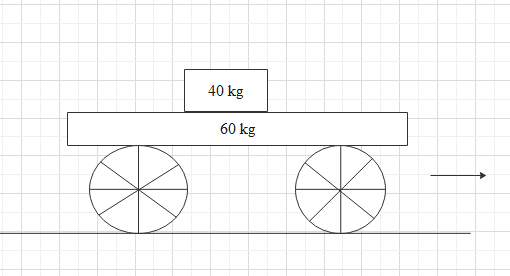
According to conservation of momentum the final momentum will be equal to the initial momentum.
Momentum is calculated as a product of mass and velocity.
$\Rightarrow P = mv$.
Where, m is the mass and v is the velocity.
Hence initial momentum is given as
$ \Rightarrow {P_i} = {m_i}{v_i}$
Final momentum is given as
$ \Rightarrow {P_f} = {m_f}{v_f}$
Now let us equate both initial and final momentum.
$ \Rightarrow {m_f}{v_f} = {m_i}{v_i}$
The final mass is
${m_f} = {m_i} + 40$
$ \Rightarrow {m_f} = 60 + 40 = 100$
On substituting the values, we get
$ \Rightarrow 100 \times {v_f} = 60 \times 2$
$ \Rightarrow {v_f} = 1.2\,\,m/s$
This is the value of final velocity.
Thus, the final kinetic energy can be calculated as
$K{E_f} = \dfrac{1}{2}{m_f}v_f^2$
On substituting the values, we get
$ \Rightarrow K{E_f} = \dfrac{1}{2} \times 100 \times {\left( {1.2} \right)^2}$
$\therefore K{E_f} = 72\,J$
This is the final kinetic energy of the system.

So, the correct answer is option B.

Note: We can apply the momentum conservation only when the net force acting on the system is zero. Here, since the trolley is moving on a smooth horizontal surface there is no effect of frictional force. When friction is also taken into consideration, we cannot apply the conservation of linear momentum.