Question

A thin spherical conducting shell of radius of radius R has a charge q. Another charge Q is placed at the center of the shell. The electrostatic potential at a point P which is at a distance $\dfrac{R}{2}$ from the center of the shell is:
A) $\dfrac{{2Q}}{{4\pi {\varepsilon _o}R}} - \dfrac{{2q}}{{4\pi {\varepsilon _o}R}}$
B) $\dfrac{{2Q}}{{4\pi {\varepsilon _o}R}} + \dfrac{{2q}}{{4\pi {\varepsilon _o}R}}$
C) $\dfrac{{Q + q}}{{4\pi {\varepsilon _o}R}} + \dfrac{2}{R}$
D) $\dfrac{{2Q}}{{4\pi {\varepsilon _o}R}}$

Answer 1

Hint: Here we just have to find the electric potential due to a hollow conducting shell. In the shell the electric potential remains the same i.e. the electric potential is uniform inside and on the shell. We have to find electric potential at point p which lies inside the shell due to charge on the surface of the shell q and the charge inside the shell Q. Hence the total potential will be the summation of the two electric potentials.

Formula Used:
$V = \dfrac{{Kq}}{R}$ ;
Where:
V= Electric Potential;
K= Proportionality Constant,$(K = \dfrac{1}{{4\pi {\varepsilon _o}}})$
q= Charge,
R= Distance.
Complete step by step answer:
Step1: Write the electric potential due to charge q and Q.

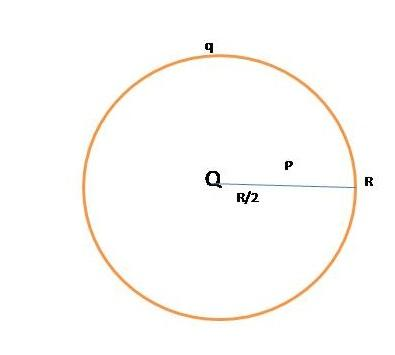
Electric potential due to q
$V = \dfrac{{Kq}}{R}$;
Put the value of R as: $R = \dfrac{R}{2}$
$\implies$ $V = \dfrac{{2Kq}}{R}$
Electric potential due to Q
$\implies$ ${V_1} = \dfrac{{KQ}}{R}$
Put the value of R as:$R = \dfrac{R}{2}$
$\implies$ ${V_1} = \dfrac{{2KQ}}{R}$;
 Step2:
Combine the two potentials to find out the total electric potential
${V_F} = V + {V_1}$
Put the values,
${V_F} = \dfrac{{2KQ}}{R} + \dfrac{{2Kq}}{R}$ ;
Put the value of K as$(K = \dfrac{1}{{4\pi {\varepsilon _o}}})$, in the above equation we have,
$V = \dfrac{{2Q}}{{4\pi {\varepsilon _o}R}} + \dfrac{{2q}}{{4\pi {\varepsilon _o}R}}$
Final Answer: The electrostatic potential at point P due to q and Q is Option B) $V = \dfrac{{2Q}}{{4\pi {\varepsilon _o}R}} + \dfrac{{2q}}{{4\pi {\varepsilon _o}R}}$.

Note: Here first find out the electric potential due to q and then electric potential due to Q. The distance between point p and charge q is (R/2) and not (R). Put the formula for electric potential, as it is uniform inside the shell it would be the same on the shell also and find the combined potential.