Question

A thermally isolated cylindrical closed vessel of height 8m is kept vertically. It is divided into two equal parts by a diathermic (perfect thermal conductor) frictionless partition of mass 8.3kg. Thus the partition is held initially at a distance of 4m from the top, as shown in the schematic figure below. Each of the two parts of the vessel contains 0.1 mole of an ideal gas at temperature 300K. The partition is now released and moves without any gas leaking from one part of the vessel to the other. When equilibrium is reached, the distance of the partition from the top (in m ) will be __________. (Take the acceleration due to gravity=\[10{\rm{ m}}{{\rm{s}}^{ - 2}}\]and the universal gas constant=\[8.3{\rm{ mo}}{{\rm{l}}^{ - 1}}{K^{ - 1}}\])

Answer 1

Hint:A thermodynamic process can be defined as a system that moves from one state to another. Here we use the ideal gas equation also called the general gas equation which gives the behaviour of many gases under many conditions.

Formula used
Ideal gas equation is given as:
\[PV = nRT\]
Where P is pressure, V is volume, n is the amount of substance, R is the universal gas constant and T is temperature.

Complete step by step solution:

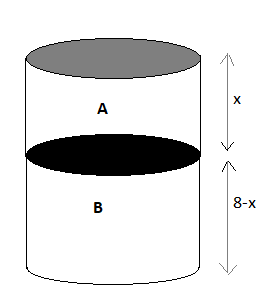
Image: A thermally isolated cylindrical closed vessel.

Let a cylindrical is divided into two equal parts by a diathermic as A and B and the distance of the partition from the top be x.
In each part of the vessel contains, number of mole of an ideal gas, n= 0.1
Temperature, T=300K

For both partition A and B after release is,
As we know ideal gas equation, \[PV = nRT\]
\[{P_A}A \times x = nRT\]
\[\begin{array}{l} \Rightarrow {P_A}(A \times x) = 0.1 \times 8.3 \times 300\\ \Rightarrow {P_A} = \dfrac{{0.1 \times 8.3 \times 300}}{{A \times x}}\end{array}\]
Similarly,
\[\begin{array}{l}{P_B}A \times (x - 8) = 0.1 \times 8.3 \times 300\\ \Rightarrow {P_B} = \dfrac{{0.1 \times 8.3 \times 300}}{{A(x - 8)}}\end{array}\]

At equilibrium condition,
\[{P_A}A + mg = {P_2}A\]
Substituting the values of \[{P_A}{\rm{ }}and{\rm{ }}{P_B}\], we get
\[\dfrac{{0.1 \times 8.3 \times 300}}{{A \times x}} + 8.3 \times 10 = \dfrac{{0.1 \times 8.3 \times 300}}{{A(x - 8)}}\]
\[{x^2} - 2x - 24 = 0\]
On solving
$\therefore x=6$

Hence when equilibrium is reached, the distance of the partition from the top will be 6m.

Note: In thermodynamics, a diathermal wall allows heat to pass through it. Whereas an adiabatic wall does not allow heat to pass through it. For a given thermodynamic process are the movement of heat energy between the systems.