Question

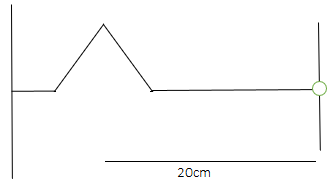
A string of linear mass density \[0.5g\,c{m^{ - 1}}\] and a total length \[30cm\] is tied to a fixed wall at one end and to a frictionless ring at the other end (figure below). The ring can move on a vertical rod. A wave pulse is produced on the string which moves towards the ring at a speed of \[20cm\,{s^{ - 1}}\]. The pulse is symmetric about its maximum which is located at a distance of \[20cm\] from the end joined to the ring.
(a) Assuming that the wave is reflected from the ends without loss of energy, find the time taken by the string to regain its shape.
(b) The shape of the string changes periodically with time. Find this time period.
(c) What is the tension in the string?

Answer 1

Hint: In this question, we see that the wire is traveling from denser to medium so phase change is equal to \[0\]. Now we know that the time is taken by the string formula is \[time = \dfrac{S}{v}\] then we find the tension of the string with the formula \[n = \dfrac{1}{{2l}}\sqrt {\left( {\dfrac{T}{m}} \right)} \,\] . So, by substituting all the given formulas we get the required result.

Formula used:
1. \[\text{Time} = \dfrac{S}{v} \]
Where, s = distance v = wave speed
2. \[n = \dfrac{1}{{2l}}\sqrt {\left( {\dfrac{T}{m}} \right)} \]
where, m = mass per unit length, l = length, T = tension of the string.

Complete step by step solution:
We are given that
mass density \[ = 0.5g\,c{m^{ - 1}}\]
total length\[ = 30cm\]
Speed \[ = 20cm\,{s^{ - 1}}\]
Now we know that the crest reflects as a crest here, as the wire is travelling from denser to rarer medium. Therefore, phase changes are equal to \[0\].
(a) Now to gain the original shape distance travelled by the wave S is
\[S = \left( {20 + 20} \right)cm = 40cm \\ \]
Now wave speed is \[v = 20m/s\]
Therefore,
\[\text{time} = \dfrac{S}{v} = \dfrac{{40}}{{20}} = 20\sec \]
Hence, the time taken is \[20\sec \]

(b) Now the wave regains its shape after travelling a periodic distance is
 \[s = 2 \times 30 = 60cm \]
Therefore,
 \[\text{time} = \dfrac{s}{v} = \dfrac{{60}}{{20}} = 3\sec \]
Hence, the time period is \[3\sec \]

(c) We know that frequency(n) is inversely proportional to time period
So,
\[n = \dfrac{1}{t} = \dfrac{1}{3}{\sec ^1} \\ \]
We know that
 \[n = \dfrac{1}{{2l}}\sqrt {\left( {\dfrac{T}{m}} \right)} \]
By substituting all the values in above, we get
\[\dfrac{1}{3} = \dfrac{1}{{2 \times 30}}\sqrt {\left( {\dfrac{T}{{0.5}}} \right)} \\
\Rightarrow \dfrac{1}{3} = \dfrac{1}{{60}}\sqrt {\left( {\dfrac{T}{{0.5}}} \right)} \\
\Rightarrow \dfrac{{60}}{3} = \sqrt {\left( {\dfrac{T}{{0.5}}} \right)} \\
\Rightarrow 20 = \sqrt {\left( {\dfrac{T}{{0.5}}} \right)} \]
Further solving, we get
\[{\left( {20} \right)^2} = {\left[ {\sqrt {\left( {\dfrac{T}{{0.5}}} \right)} } \right]^2} \\
\Rightarrow 400 = \dfrac{T}{{0.5}} \\
\Rightarrow T = 400 \times 0.5 = 400 \times \dfrac{5}{{10}} \]
Furthermore solving,
\[T = 40 \times 5 \\
\Rightarrow T = 200dyne \\
\Rightarrow T = 2 \times {10^{ - 3}}Newton \]
Hence, tension in the string is \[2 \times {10^{ - 3}}Newton\]

Note: Students must understand all of the formulas used in the solution and be careful when substituting all of the values in the formula; otherwise, calculation errors may occur, and students will not obtain the desired result.