Question

A straight line passes through a point \[\left( {1,1} \right)\]. Meets the X-axis at \[A\] and the Y-axis at \[B\]. Then what is the locus of the mid-point of \[AB\]?
A. \[2xy + x + y = 0\]
B. \[x + y - 2xy = 0\]
C. \[x + y + 2 = 0\]
D. \[x + y - 2 = 0\]

Answer 1

Hint: Since the point \[A\] lie on \[x\] axis, assuming the coordinate as \[\left( {a,0} \right)\]. Since \[B\] lie on \[y\] axis, assuming the coordinate as \[\left( {0,b} \right)\]. By using the intercepts form of a line \[\dfrac{x}{p} + \dfrac{y}{q} = 1\], we will find the equation of line \[AB\]. Then put \[\left( {1,1} \right)\] in the equation of line. Assume the coordinate of midpoint of \[AB\]. Then calculate the value of \[a\] and \[b\] in terms of \[h\] and \[k\]. Then substitute the value of \[a\] and \[b\] in the equation of line. To get the locus of the midpoint, replace \[h\] by \[x\] and \[k\] by \[y\].

Formula used:
The mid-point of the line joining the points \[\left( {{x_1},{y_1}} \right)\] and \[\left( {{x_2},{y_2}} \right)\] is: \[\left( {x,y} \right) = \left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right)\]
The intercept form of an equation of a line is \[\dfrac{x}{p} + \dfrac{y}{q} = 1\], where \[p\] is x-intercept and \[q\] is y-intercept.

Complete step by step solution:
Given: The line passes through the point \[\left( {1,1} \right)\] and intersect the X-axis at \[A\] and Y-axis at \[B\].
Let \[A\left( {a,0} \right)\] be the x-intercept and \[B\left( {0,b} \right)\] be the y-intercept of the line.

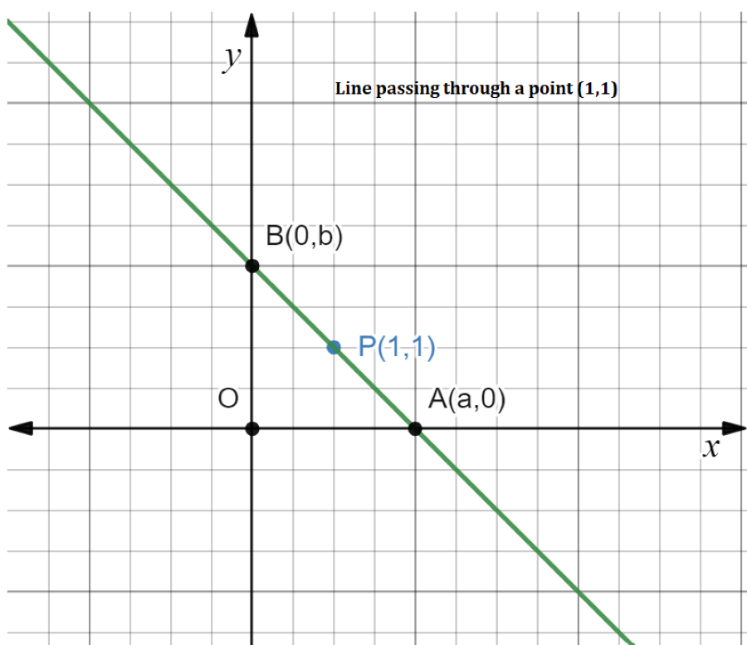
Let’s form the equation of line using the intercept form.
\[\dfrac{x}{a} + \dfrac{y}{b} = 1\]
Since the line passes through the point \[P\left( {1,1} \right)\].
So, the point satisfies the equation of line.
 \[\dfrac{1}{a} + \dfrac{1}{b} = 1\]
\[ \Rightarrow \]\[\dfrac{{b + a}}{{ab}} = 1\]
\[ \Rightarrow \]\[a + b = ab\] \[.....\left( 1 \right)\]
Let consider \[Q\left( {h,k} \right)\] be the mid-point of \[AB\].
Apply mid-point formula to calculate the coordinates of \[Q\left( {h,k} \right)\].
Then,
\[\left( {h,k} \right) = \left( {\dfrac{{a + 0}}{2},\dfrac{{0 + b}}{2}} \right)\]
\[ \Rightarrow \]\[\left( {h,k} \right) = \left( {\dfrac{a}{2},\dfrac{b}{2}} \right)\]
Now compare the coordinates.
\[h = \dfrac{a}{2}\] and \[k = \dfrac{b}{2}\]
\[ \Rightarrow \]\[a = 2h\] and \[b = 2k\]
Substitute the above values in equation \[\left( 1 \right)\].
\[2h + 2k = \left( {2h} \right)\left( {2k} \right)\]
Simplify the equation.
\[2h + 2k = 4hk\]
\[ \Rightarrow \]\[h + k = 2hk\]
\[ \Rightarrow \]\[h + k - 2hk = 0\]
Therefore, the equation of locus is \[x + y - 2xy = 0\]

Hence the correct option is B.

Note: A locus is a set of points that satisfy a specific condition for a geometric shape or figure.
Steps to calculate the equation of locus:
Assume the locus point.
Use distance, section and other formulas that satisfy the condition.
Substitute the values in the specific condition and simplify the equation.