
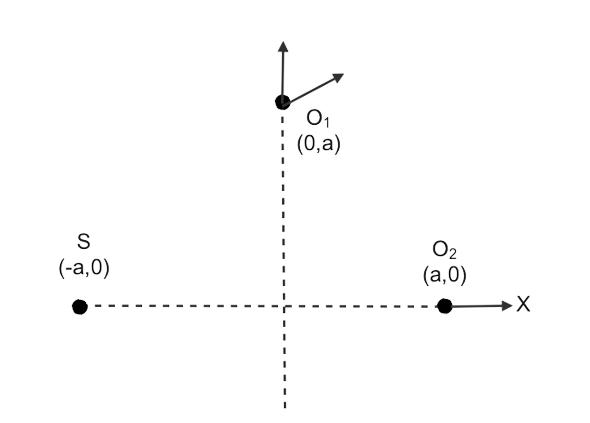
A sound source S and observers O1, O2 are placed as shown S is always at rest and $O_1$, $O_2$ start moving with velocity $v_0$ at t=0. At t=5 sec, $f_1$ and $f_2$ represent apparent frequencies of sound received by $O_1$ and $O_2$ respectively. The ratio of $f_1$ and $f_2$ is:
A. Zero
B. Between 0 and 1
C. 1
D. >1
Answer
186.9k+ views
Hint: To solve this question we will use the concept of doppler effect. Here we will need the relative speed of sound waves when the listener and sources are in motion with respect to each other. With the help of the equation for apparent frequency one can easily solve this problem.
Formula used:
The equation of apparent frequency in doppler effect is:
${f^{'}}=f\left( \dfrac{v-{{v}_{0}}}{v-{{v}_{s}}} \right)$
Complete answer:
For a listener, sound waves are the disturbance of air around his ears and the pressure varies between maximum and minimum. The pitch of the sound heard by the observer depends on this pressure variation.
If the observer or source or both are in motion with respect to each other, the frequency observed will be different from that of the frequency of source. This apparent change in frequency of wave due to motion of the observer or source is called doppler effect.
The general equation for apparent frequency in doppler effect is:
${f^{'}}=f\left( \dfrac{v-{{v}_{0}}}{v-{{v}_{s}}} \right)$
Where,
${f^’}$ is the apparent frequency
f is the actual frequency
v is the velocity of sound in air
$v_0$ is the velocity of observer
$v_s$ is the velocity of the source
In this question the velocity of the source is zero since the source is at rest. For observer 1, if $\theta$ is the angle between the axis and velocity of sound then the velocity of observer is ${v_0} \cos \theta$.
Then the apparent frequency of observer 1 is:
${{f}_{1}}=\dfrac{v-{{v}_{0}}\cos \theta }{v}-(1)$
The apparent frequency of observer 2 is:
${{f}_{2}}=\dfrac{v-{{v}_{0}}}{v}-(2)$
$\therefore \dfrac{{{f}_{_{1}}}}{{{f}_{2}}}=\dfrac{v-{{v}_{0}}\cos \theta }{v-{{v}_{0}}}$
And we all know that the maximum value of cosϴ is always greater than or equal to one.
\[\therefore \dfrac{{{f}_{1}}}{{{f}_{2}}}>1\]
Therefore, the answer is (D).
Note: In the doppler effect we are only concerned about relative motion between source and observer when the numerator is larger than the denominator then the ratio will always be greater than one.
Formula used:
The equation of apparent frequency in doppler effect is:
${f^{'}}=f\left( \dfrac{v-{{v}_{0}}}{v-{{v}_{s}}} \right)$
Complete answer:

For a listener, sound waves are the disturbance of air around his ears and the pressure varies between maximum and minimum. The pitch of the sound heard by the observer depends on this pressure variation.
If the observer or source or both are in motion with respect to each other, the frequency observed will be different from that of the frequency of source. This apparent change in frequency of wave due to motion of the observer or source is called doppler effect.
The general equation for apparent frequency in doppler effect is:
${f^{'}}=f\left( \dfrac{v-{{v}_{0}}}{v-{{v}_{s}}} \right)$
Where,
${f^’}$ is the apparent frequency
f is the actual frequency
v is the velocity of sound in air
$v_0$ is the velocity of observer
$v_s$ is the velocity of the source
In this question the velocity of the source is zero since the source is at rest. For observer 1, if $\theta$ is the angle between the axis and velocity of sound then the velocity of observer is ${v_0} \cos \theta$.
Then the apparent frequency of observer 1 is:
${{f}_{1}}=\dfrac{v-{{v}_{0}}\cos \theta }{v}-(1)$
The apparent frequency of observer 2 is:
${{f}_{2}}=\dfrac{v-{{v}_{0}}}{v}-(2)$
$\therefore \dfrac{{{f}_{_{1}}}}{{{f}_{2}}}=\dfrac{v-{{v}_{0}}\cos \theta }{v-{{v}_{0}}}$
And we all know that the maximum value of cosϴ is always greater than or equal to one.
\[\therefore \dfrac{{{f}_{1}}}{{{f}_{2}}}>1\]
Therefore, the answer is (D).
Note: In the doppler effect we are only concerned about relative motion between source and observer when the numerator is larger than the denominator then the ratio will always be greater than one.
Recently Updated Pages
Uniform Acceleration: Definition, Equations & Graphs for JEE/NEET

JEE Isolation, Preparation and Properties of Non-metals Important Concepts and Tips for Exam Preparation

JEE Energetics Important Concepts and Tips for Exam Preparation

JEE Extractive Metallurgy Important Concepts and Tips for Exam Preparation

JEE Electricity and Magnetism Important Concepts and Tips for Exam Preparation

Electrical Resistance - Important Concepts and Tips for JEE

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

Equation of Trajectory in Projectile Motion: Derivation & Proof

Atomic Structure: Definition, Models, and Examples

Angle of Deviation in a Prism – Formula, Diagram & Applications

Hybridisation in Chemistry – Concept, Types & Applications

Collision: Meaning, Types & Examples in Physics

Other Pages
NCERT Solutions For Class 11 Physics Chapter 2 Motion In A Straight Line - 2025-26

NCERT Solutions For Class 11 Physics Chapter 1 Units and Measurements - 2025-26

NCERT Solutions For Class 11 Physics Chapter 3 Motion In A Plane - 2025-26

JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26

Motion in a Straight Line Class 11 Physics Chapter 2 CBSE Notes - 2025-26




