Question

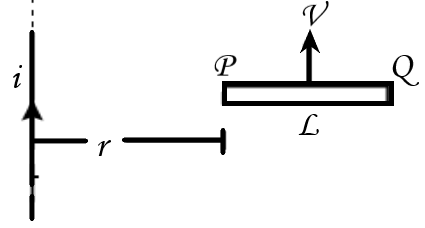
A rod $PQ$ of length $L$ moves with a uniform velocity $v$ parallel to a long straight wire carrying a current $i$. The end $P$ of the rod always remains at a distance $r$ from the wire. Calculate the emf induced across the rod. Take, $v = 5.0m/s,i = 100A,\,r = 1.0cm\;$ and $L = 19cm,lo{g_e}20 = 3$.

A. $7 \times {10^{ - 4}}V$
B. $5 \times {10^{ - 4}}V$
C. $3 \times {10^{ - 4}}V$
D. $1 \times {10^{ - 4}}V$

Answer 1

Hint: According to Faraday's law, an electromotive force is generated in a circuit at a rate proportionate to the rate at which the magnetic flux linking it changes. We know that Faraday’s law of induction is given by $\varepsilon = - \dfrac{{d{\phi _B}}}{{dt}}$, Where $\varepsilon $ is the induced emf and ${\phi _B}$ is the magnetic flux defined by ${\phi _B} = \oint {\vec B \cdot \vec dS} $. Here, $\vec B$ is the magnetic field.

Complete step by step solution:
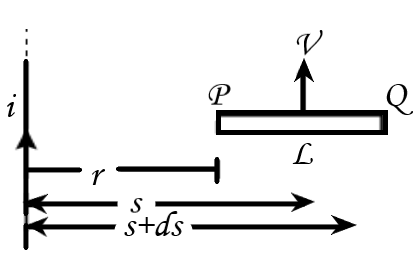
In the question, the rod $PQ$ is moving in the magnetic field, produced by the long, straight current-carrying wire. As we know that, the field does not remain constant along the entire length of the rod or change with distance. Let us consider a small element $ds$ at distance $s$ from a wire.


In order to calculate the magnetic flux, we first need to calculate the magnetic field by using Ampere’s law,
$\oint {\vec B \cdot \vec dS} = {\mu _0}I$
We find that the magnetic field of the wire carrying the current at a distance from the wire is:
$B2s\pi = {\mu _0}I \\$
$\Rightarrow B = \dfrac{{{\mu _0}I}}{{2s\pi }}$
Around the wire, the magnetic field's lines form concentric rings. Given that the infinitesimal area vector is pointed in the same direction as the wire's normal:
${\phi _B} = \oint {\vec B \cdot \vec dS} \\
\Rightarrow {\phi _B} = \oint {BdS} $
If magnetic field at the position of $ds$ is $B$ then induced emf in this element is:
${\phi _B} = Bv(ds) = \dfrac{{{\mu _0}i}}{{2\pi s}}v(ds)$

Now, induced emf in the entire length of the rod $PQ$ is:
$\int {{\phi _B}} = \int\limits_{{s_P}}^{{s_Q}} {\dfrac{{{\mu _0}i}}{{2\pi s}}v(ds)} $
At $P$, we have ${s_P} = r$ and at $Q$, $\;{s_Q} = r + L$ then:
$\phi = \dfrac{{{\mu _0}iv}}{{2\pi }}\int\limits_r^{r + L} {\dfrac{{ds}}{s}} \\$
$\Rightarrow \phi = \dfrac{{{\mu _0}iv}}{{2\pi }}[{\log _e}s]_r^{r + L} \\$
$\Rightarrow \phi = \dfrac{{{\mu _0}iv}}{{2\pi }}[{\log _e}(r + L) - {\log _e}r] \\$
$\Rightarrow \phi = \dfrac{{{\mu _0}iv}}{{2\pi }}\log [1 + \dfrac{L}{r}]$
Now, substitute all the given values in the obtained equation, we obtain:
$\phi = (2 \times {10^{ - 7}})(100)(5.0)\log (1 + \dfrac{{19}}{1}) \\$
$\therefore \phi = 3 \times {10^{ - 4}}V$

Therefore, the correct option is C.

Note: In order to use the magnetic flux, we therefore determined the magnetic field. In certain circumstances, EMF is produced by the movement of a conductor in a magnetic field. Due to the long straight wire's magnetic field's variable $s$.