Question

A rod AB of mass \[10Kg\] and length \[4m\] rests on a horizontal floor with end A fixed so, as to rotate it in a vertical plane about a perpendicular axis passing through A. If the work done on the rod is \[100J\], the height to which the end B be raised vertically above the floor is?

Answer 1

Hint:Before proceeding with the question first we need to know how the work has been applied to a rod. Assuming a rod which has been lifted up and one of its ends is in contact with the ground and the other is the uniform end. In a conservative field of force, work is path independent.

Formula used:
Expression of Work done is,
\[W = F \times d\]
Where, Work done on the rod is given as \[100J\]. F is the force applied on the rod and d is the displacement done by the rod.

Complete step by step solution:
Considering the figure below,

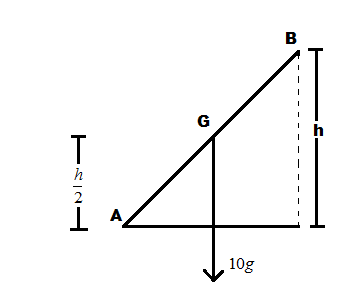
Here, as we know, the value for the work done on the rod is given as \[100J\].
We know the formula,
\[F = mg\]
Where, \[m\] is mass and \[g\] is the acceleration due to gravity.
Hence we can write work done,
\[W = F \times d\\
\Rightarrow W = \left( {mg} \right) \times d\]
Here, displacement is equal to \[\dfrac{h}{2}\]
Therefore, we can write
\[\begin{array}{l}W = \left( {mg} \right) \times d\\ \Rightarrow W = \left( {mg} \right) \times \dfrac{h}{2}\\\Rightarrow 100 = \dfrac{{10 \times 10 \times h}}{2}\end{array}\]
On solving this, we get
 \[h = 2m\]

Hence, the height to which the end B be raised vertically above the floor is \[2m\] respectively.

Note: As we know, work is path independent, and assuming a rod which has been lifted up and one of its ends is in contact with the ground and the other is the uniform end we calculated the required height to which the end B be raised vertically above the floor.