Question

A reaction of \[0.1\] mole of benzyl amine with bromomethane gave \[23g\] of benzyl trimethyl ammonium bromide. The number of moles of bromomethane consumed in this reaction are \[n \times {10^{ - 1}}\] , when \[n = \] _______. (Round off to the Nearest Integer). [Given: Atomic masses: C: \[12.0{\text{ }}u\] , H: \[1.0{\text{ }}u\], N: \[14.0{\text{ }}u\], Br: \[80.0{\text{ }}u\] ]

Answer 1

Hint: The structure of benzyl amine is as follows:

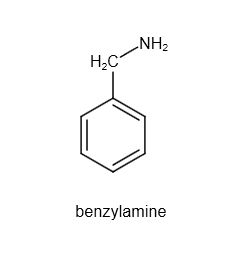
Image: Structure of benzylamine
The structure of benzyl trimethyl ammonium bromide is as follows:

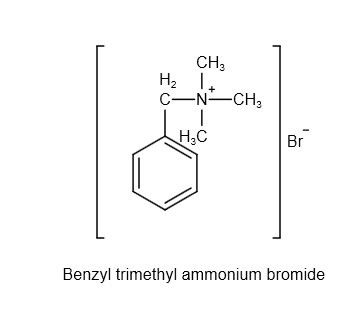
Image: structure of benzyl trimethyl ammonium bromide

Complete Step by Step Solution:
There is a reaction between benzylamine and bromoethane produces benzyl trimethyl ammonium bromide. The balanced chemical reaction is as follows:


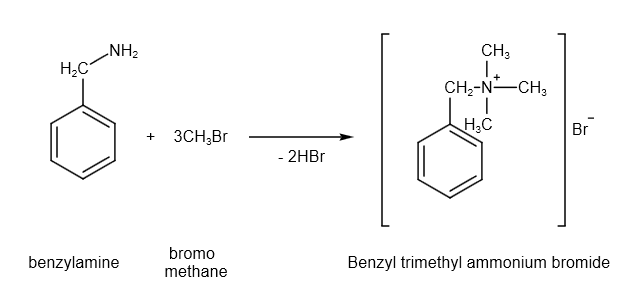
Image: reaction between benzylamine and bromomethane
From the reaction stoichiometry, one mole of benzylamine reacts with three moles of bromomethane and produces one mole of benzyl trimethyl ammonium bromide.
Here, \[0.1\] mole of benzyl amine reacts with bromomethane and gave \[23g\] of benzyl trimethyl ammonium bromide.
First of all, we have to calculate the molar mass of benzyl trimethyl ammonium bromide.
From the structure, the chemical formula of benzyl trimethyl ammonium bromide is \[{C_{10}}{H_{16}}NBr\] .
Calculate the molar mass of \[{C_{10}}{H_{16}}NBr\] from the given atomic masses as follows:
\[
  {\text{molar mass of }}{C_{10}}{H_{16}}NBr = 10\left( {12.0} \right) + 16\left( {1.0} \right) + 14.0 + 80.0 \\
   \Rightarrow {\text{molar mass of }}{C_{10}}{H_{16}}NBr = 230 \\
 \]
Therefore, the molar mass of \[{C_{10}}{H_{16}}NBr\] is \[230\].
We have to calculate the moles of \[{C_{10}}{H_{16}}NBr\] from given mass ( \[23g\] ).
We know that,
\[n = \dfrac{{weight}}{{mol.mass}}\]
Substituting the values,
\[
  {n_{{C_{10}}{H_{16}}NBr}} = \dfrac{{23}}{{230}} \\
   \Rightarrow {n_{{C_{10}}{H_{16}}NBr}} = 0.1 \\
 \]
From the reaction stoichiometry,
\[1\] mole of \[{C_{10}}{H_{16}}NBr\] formed from \[3\] moles of bromomethane.
Calculate the number of moles of bromomethane requires for \[0.1\] mole of \[{C_{10}}{H_{16}}NBr\] formation as follows:
\[
  {n_{C{H_3}Br}} = 0.1{\text{ }} \times \dfrac{3}{1} \\
   \Rightarrow {n_{C{H_3}Br}} = 0.3 \\
 \]
The number of moles consumed in the reaction are \[n \times {10^{ - 1}}\] .
So, we can say that,
\[
  n \times {10^{ - 1}} = {n_{C{H_3}Br}} \\
   \Rightarrow n \times {10^{ - 1}} = 0.3 \\
   \Rightarrow n = 3 \\
 \]
Therefore, the value of \[n\] is \[3\] .

Note: Mole, or mol, is a common scientific unit in chemistry that is used to measure vast amounts of tiny objects such as molecules, atoms, or other particles. The number of moles of a solute in a litre of solution is known as molarity. A mole is a unit of measurement that helps us match the particles of a substance to its mass. The molecular weight, also known as molar mass, is the sum of the masses of each atom in grammes that make up a mole of a molecule.