Question

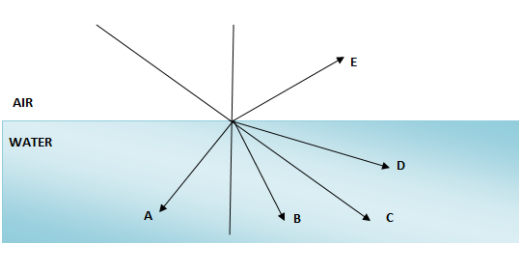
A ray of light from air suffers partial reflection and refraction at the boundary of water. In the figure, which of the rays A, B, C, D and E are the correct (i) refracted ray (ii) partially reflected ray?



(A) A
(B) B
(C) C
(D) D

Answer 1

Hint: As the medium of propagation of light is changing, this would lead to a refractive index of mediums and hence the light will change in the path depending on respective refractive indices. When the light ray returns back in the same medium, this is reflection. Use this law for partially reflected and Snell’s law for refracted rays.

Complete step by step answer:
We have been given a figure of rays A, B, C, D and E.
We know from Snell’s law that partial Reflection and Refraction occurs when a light ray is travelling between two mediums. Some of the ray is reflected back and the rest is refracted through into the other medium. The sun reflects part of its light off of the water, and the rest it refracts into the water.
Also, when the light ray is incident on a surface while travelling from lower density medium to higher density medium, the refracted ray bends towards the normal of incidence. But the refracted ray moves away from the normal of the incidence if the light ray is travelling from higher density to lower density medium.

(i) As we know that water is denser than air. So, using the above mentioned concept, if a light ray is travelling from air to water, the refracted ray should bend towards the normal of incidence. From the figure given in the question, we can see that B is the only ray which is bent towards normal. C is more or less at the angle from normal and D is moving away from the normal. Thus, B is the correct refracted ray.
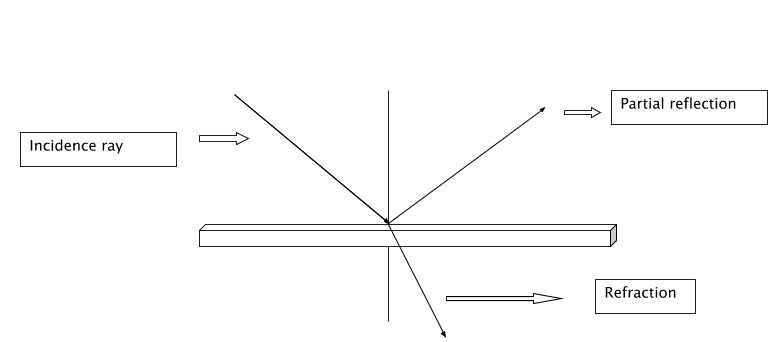
(ii) A figure is shown above for a clear explanation of partially reflected rays. When we compare this figure with the one given in the question we can say that ray E is the partially reflected ray, as reflection of light takes place in the same medium.
So correct option for (i) is option B
So correct option for (ii) is option E

Note: When the refracted ray makes an angle of ${90^ \circ }$ with the normal at incidence then the angle of incidence in this case is called critical angle and it is given by the formula:
$ \Rightarrow {\theta _c} = {\sin ^{ - 1}}\left( {\dfrac{{{\mu _2}}}{{{\mu _1}}}} \right)$, where ${\theta _c}$ is the critical angle, ${\mu _1}$ is the refractive index of first medium and ${\mu _2}$ is the refractive index of second medium.
This scenario can occur only when the light is travelling from denser medium (refractive index ${\mu _1}$) to rarer medium (refractive index ${\mu _2}$) because only in that case the refracted ray bends away from the normal. Therefore we have:
$ \Rightarrow {\mu _1} > {\mu _2}$ and $\sin {\theta _c} < 1$.