
A point source of light is placed at a depth of $h$ below the surface of water of refractive index $\mu $. A floating opaque disc is placed on the surface of water so that light from the source is not visible from the surface. The minimum diameter of the disc is
A. $\dfrac{{2h}}{{{{({\mu ^2} - 1)}^{\dfrac{1}{2}}}}}$
B. $2h{({\mu ^2} - 1)^{\dfrac{1}{2}}}$
C. $\dfrac{h}{{2{{({\mu ^2} - 1)}^{\dfrac{1}{2}}}}}$
D. $h{({\mu ^2} - 1)^{\dfrac{1}{2}}}$
Answer
204.9k+ views
Hint: The light ray will refract back if the incidence angle becomes greater than the critical angle and hence we will use this concept to find the disc diameter. Use basic trigonometry to further solve the question.
Formula used:
${\theta _c} = {\sin ^{ - 1}}\left( {\dfrac{1}{\mu }} \right) \\$
Complete Step-by-Step Explanation:
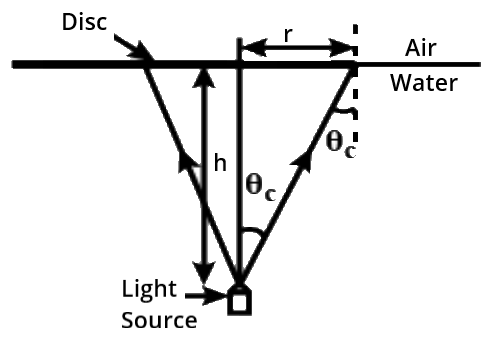
The above illustration depicts incidence from water at a critical angle ${\theta _c}$ limiting angle,
Consequently, the following formula provides the critical angle of a medium:
${\theta _c} = {\sin ^{ - 1}}\left( {\dfrac{1}{\mu }} \right) \\$
$\sin {\theta _c} = \dfrac{1}{\mu } \\$
So that, from the relation in the above equation, the equation can be written as:
$\tan {\theta _c} = \dfrac{1}{{{{({\mu ^2} - 1)}^{\dfrac{1}{2}}}}} \Rightarrow \dfrac{r}{h}$
Where, $r$be the radius of the disc,
Therefore, the diameter of the disc is:
$2r = 2h\,\tan {\theta _c} \\$
$\Rightarrow d = \dfrac{{2h}}{{{{({\mu ^2} - 1)}^{\dfrac{1}{2}}}}} \\$
Thus, the correct option is: (A) $\dfrac{{2h}}{{{{({\mu ^2} - 1)}^{\dfrac{1}{2}}}}}$
Note: for such questions you should be clear with the concept of critical angle and basic laws of refraction. Remember when light goes from denser to rarer the snell’s law applied in opposite manner as compared to the one we study conventionally.
Formula used:
${\theta _c} = {\sin ^{ - 1}}\left( {\dfrac{1}{\mu }} \right) \\$
Complete Step-by-Step Explanation:

The above illustration depicts incidence from water at a critical angle ${\theta _c}$ limiting angle,
Consequently, the following formula provides the critical angle of a medium:
${\theta _c} = {\sin ^{ - 1}}\left( {\dfrac{1}{\mu }} \right) \\$
$\sin {\theta _c} = \dfrac{1}{\mu } \\$
So that, from the relation in the above equation, the equation can be written as:
$\tan {\theta _c} = \dfrac{1}{{{{({\mu ^2} - 1)}^{\dfrac{1}{2}}}}} \Rightarrow \dfrac{r}{h}$
Where, $r$be the radius of the disc,
Therefore, the diameter of the disc is:
$2r = 2h\,\tan {\theta _c} \\$
$\Rightarrow d = \dfrac{{2h}}{{{{({\mu ^2} - 1)}^{\dfrac{1}{2}}}}} \\$
Thus, the correct option is: (A) $\dfrac{{2h}}{{{{({\mu ^2} - 1)}^{\dfrac{1}{2}}}}}$
Note: for such questions you should be clear with the concept of critical angle and basic laws of refraction. Remember when light goes from denser to rarer the snell’s law applied in opposite manner as compared to the one we study conventionally.
Recently Updated Pages
JEE Main 2026: Exam Dates OUT, Registration Open, Syllabus & Eligibility

JEE Main Candidate Login 2026 and Registration Portal | Form Access

Household Electricity Important Concepts and Tips for JEE

JEE Main 2023 (January 31st Shift 1) Physics Question Paper with Answer Key

Clemmensen and Wolff Kishner Reduction - Important Concepts and Tips for JEE

JEE Main Maths Paper Pattern 2026: Marking Scheme & Sections

Trending doubts
Ideal and Non-Ideal Solutions Explained for Class 12 Chemistry

Centre of Mass of Hollow and Solid Hemisphere Explained

Wheatstone Bridge Explained: Principle, Working, and Uses

Charging and Discharging of Capacitor Explained

Young's Double Slit Experiment Derivation: Formula, Steps & Diagram

Elastic Collision in Two Dimensions: Concepts, Laws, Derivation & Examples

Other Pages
JEE Advanced 2025: Dates, Registration, Syllabus, Eligibility Criteria and More

Diffraction of Light - Young’s Single Slit Experiment

Chemistry Question Papers for JEE Main, NEET & Boards (PDFs)

Devuthani Ekadashi 2025: Correct Date, Shubh Muhurat, Parana Time & Puja Vidhi

Halloween 2025: Date, History, Significance, and Traditions

JEE Main 2026: Exam Date, Syllabus, Eligibility, Registration and Preparation




