Question

A network of six identical capacitors, each of capacitance $C$ is formed as shown below. The equivalent capacitance between the point A and B is:

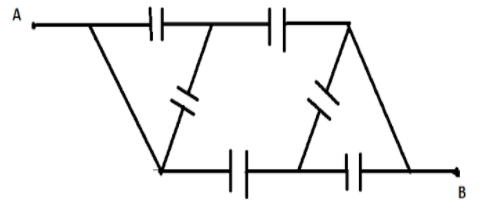
Answer 1

Hint: To solve this question we have first made this circuit simpler. For that we have to break the circuit in simpler parts and then solve for the capacitance in that part. After that we have to find all the capacitance connected in series and in parallel and then find the equivalent capacitance.

Formulae used:
${C_{eq}} = {C_1} + {C_2}$
Here ${C_{eq}}$ is the equivalent capacitance in parallel connection and ${C_1}$ and ${C_2}$ are the capacitors are connected in parallel.
$\dfrac{1}{{{C_{eq}}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}}$
Here ${C_{eq}}$ is the equivalent capacitance in series connection and ${C_1}$ and ${C_2}$ are the capacitors that are connected in series.

Complete step by step answer:
In the question, a complicated circuit diagram which consists of capacitors is given.

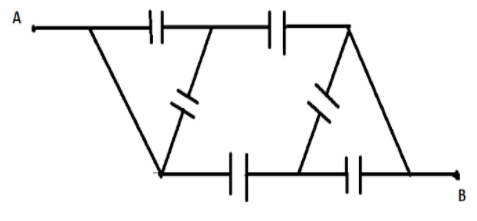
Let’s simplify this diagram.

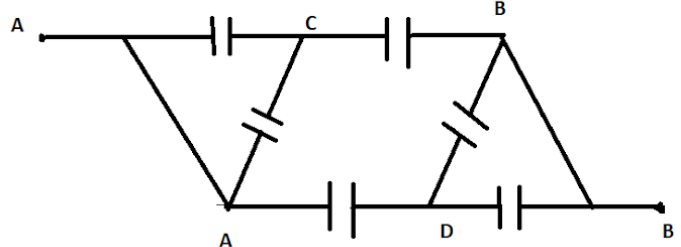
The points are named according to the presence of capacitors. If no capacitor is present between two points then they are named the same but if a capacitor is present then the name is changed. Like there is no capacitor between path AA so the name is kept the same whereas in path AD, a capacitor is present so the name is changed.
The above diagram can be further simplified.

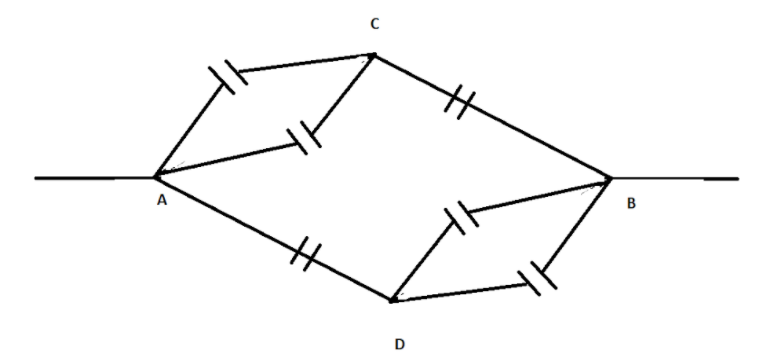
From the above figure we can say that,
1. The capacitors between AC and BD are in parallel.
2. The capacitors in path ACB and ADB are in series.
3. The capacitors in between A and B are in parallel.
So the equivalent capacitor between Path AC and BD.
We know that
$ \Rightarrow {C_{eq}} = {C_1} + {C_2}$
Here ${C_{eq}}$ is the equivalent capacitance in parallel connection and ${C_1}$ and ${C_2}$ are the capacitors are connected in parallel.
In the question the capacitance of the capacitors are given as $C$.
So,
$ \Rightarrow {C_{AC}} = C + C = 2C$
As BD has a similar type of connection the capacitance along it will also be the same. Hence,
$ \Rightarrow {C_{BD}} = 2C$

Path ACB and ADB
We know that,
$ \Rightarrow \dfrac{1}{{{C_{ACB}}}} = \dfrac{1}{{{C_{AC}}}} + \dfrac{1}{{{C_{CB}}}}$
Here ${C_{eq}}$ is the equivalent capacitance in series connection and ${C_{AC}}$ and ${C_{CB}}$ are the capacitors are connected in series.
$ \Rightarrow \dfrac{1}{{{C_{ACB}}}} = \dfrac{1}{{2C}} + \dfrac{1}{C}$
$ \Rightarrow {C_{ACB}} = \dfrac{2}{3}C$

Path ADB has similar arrangement so the capacitance along it will also be the same. Hence,
$ \Rightarrow {C_{ADB}} = \dfrac{2}{3}C$
A and B
We know that,
$ \Rightarrow {C_{eq}} = {C_1} + {C_2}$
Here ${C_{eq}}$ is the equivalent capacitance in parallel connection and ${C_1}$ and ${C_2}$ are the capacitors are connected in parallel.
$ \Rightarrow {C_{AB}} = {C_{ACB}} + {C_{ADB}}$
$ \Rightarrow {C_{AB}} = \dfrac{2}{3}C + \dfrac{2}{3}C = \dfrac{4}{3}C$

So the equivalent capacitance between A and B will be $\dfrac{2}{3}C$.

Note: While calculating the capacitance of the capacitors we should always be very careful about the type of connection. Always use the correct formula for calculating the series and parallel connections. Also try to simplify the circuit to make calculation easy.