Question

A man of mass $90kg $ is standing in an elevator whose cable broke suddenly. If the elevator falls, apparent weight of the man is-
(A) $90N $
(b) $90gN $
(c) $0N $
(d) Any negative value

Answer 1

Hint When the elevator is stationary, the weight of the man will be his mass times the gravitational acceleration. The weight is equal to the normal contact force which is experienced by the man on the floor of the elevator.

Complete Step by step answer
There are two ways to solve this question-
From an inertial frame of reference-
When the man and the elevator are observed from an inertial frame of reference, which is the ground. It can be observed that after the cable breaks, the lift starts to fall freely.
It is given that the mass of the man is, $m = 90kg $
Let the N be the normal reaction force, then it is given by,

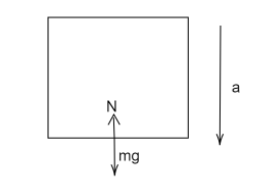
 $\vec N - m\vec g = m\vec a $
When the elevator is not moving, the acceleration, $a = 0 $
 $N = 90 \times 10 $
Therefore force exerted by the man when the elevator is stationary the contact force (which is equal to the weight of the object), $N = 900N $
(taking, $g = 10m/{s^2} $)
When the elevator starts to fall freely, the acceleration becomes,
 $a = g = 10m/{s^2} $
On balancing the forces,
 $\vec N = m\vec g + m\vec a $
Since acceleration is downwards, it has a negative sign.
 $N = mg - ma $
Substituting the value of $a $,
 $N = mg - mg $
 $N = 0 $

From non-inertial frame of reference
When the calculations are done from a non-inertial frame of reference, which is from inside the elevator. The acceleration of the frame of reference is also taken into account.
A pseudo force, equal to mass of the body times the acceleration of the frame acts in the direction opposite to the motion of the frame.
The free-body diagram looks like this-

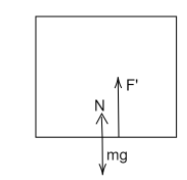
Thus the normal force can be defined as-
 $N + F' = mg $
 $N = mg - F' $
We know that the pseudo force, $F' = mg $
Therefore,
 $N = mg - mg $
 $N = 0 $
Therefore the apparent weight of the object is zero.

Option (C) is correct.

Note
There are two types of frames of reference- inertial and non-inertial. The inertial frame of reference is either at rest or is moving with a constant velocity. Whereas a non-inertial frame of reference is accelerating. In a non-inertial frame, every object experiences a pseudo force which is in the direction opposite to the acceleration of the frame.