Question

A man is observing, from the top of a tower, a boat speeding towards the tower from a certain point \[A\], with uniform speed. At that point, the angle of depression of the boat with the man’s eye is \[30^\circ \] (Ignore man’s height). After sailing for \[20\] seconds towards the base of the tower (which is at the level of water), the boat has reached point \[B\], where the angle of depression is \[45^\circ \]. Then the time taken (in seconds) by the boat from \[B\] to reach the base of the tower is
A. \[10\left( {\sqrt 3 - 1} \right)\]
B. \[10\sqrt 3 \]
C. \[10\]
D. \[10\left( {\sqrt 3 + 1} \right)\]

Answer 1

Hint: Please see the below image for reference. Let \[P\] be the position of the man on the top of the tower and \[Q\] be the foot of the tower. Then the points \[A,B,Q\] are collinear and \[PQ \bot AQ\]. Let \[AB = x\], \[BQ = y\], \[PQ = h\]. By the condition, \[\angle PAQ = 30^\circ \] and \[\angle PBQ = 45^\circ \]. The triangles \[PAQ\] and \[PBQ\] are right-angled. First, use the trigonometric ratios to find \[y\] in terms of \[x\] and to calculate the speed of the boat. Then using the relationship between speed, distance, and time, find the required time.

Formula Used:
\[\tan \theta = \dfrac{{height}}{{base}}\]
\[speed = \dfrac{{dis\tan ce}}{{time}}\]

Complete step-by-step answer:
Given that \[A\] is the initial position of the boat speeding towards a tower and \[B\] is the position of the boat after sailing for \[20\] seconds towards the base of the tower.
Let \[P\] be the position of the man on the top of the tower and \[Q\] be the foot of the tower, which is at the level of water.
Then the points \[A,B,Q\] are collinear and \[PQ \bot AQ\]
Let \[x\] be the distance of the two points \[A\] and \[B\] and \[y\] be the distance of the point \[B\] from the foot of the tower \[Q\].
Also, let \[h\] be the height of the tower.

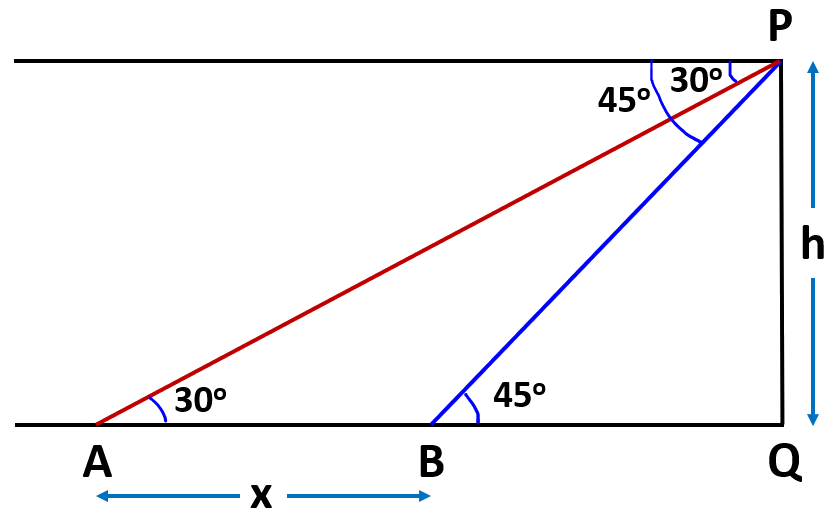
Then \[AB = x\], \[BQ = y\], \[PQ = h\], \[\angle PAQ = 30^\circ \] and \[\angle PBQ = 45^\circ \]
From triangle \[PAQ\],
\[\dfrac{{PQ}}{{AQ}} = \tan 30^\circ \]
\[ \Rightarrow \dfrac{h}{{x + y}} = \dfrac{1}{{\sqrt 3 }}\]
\[ \Rightarrow x + y = \sqrt 3 h - - - - - \left( i \right)\]
From triangle \[PBQ\],
\[\dfrac{{PQ}}{{BQ}} = \tan 45^\circ \]
\[ \Rightarrow \dfrac{h}{y} = 1\]
\[ \Rightarrow h = y - - - - - \left( {ii} \right)\]
From equations \[\left( i \right)\] and \[\left( {ii} \right)\], we get
\[x + y = \sqrt 3 y\]
\[ \Rightarrow \sqrt 3 y - y = x\]
\[ \Rightarrow \left( {\sqrt 3 - 1} \right)y = x\]
\[ \Rightarrow y = \dfrac{x}{{\sqrt 3 - 1}}\]
After rationalization of denominator, we get,
\[ \Rightarrow y = \dfrac{{x\left( {\sqrt 3 + 1} \right)}}{{\left( {\sqrt 3 - 1} \right)\left( {\sqrt 3 + 1} \right)}}\]
Identity $(a-b)(a+b)=a^2-b^2$
\[ \Rightarrow y = \dfrac{{x\left( {\sqrt 3 + 1} \right)}}{{{{\left( {\sqrt 3 } \right)}^2} - {{\left( 1 \right)}^2}}}\]
\[ \Rightarrow y = \dfrac{{x\left( {\sqrt 3 + 1} \right)}}{{3 - 1}}\]
\[ \Rightarrow y = \dfrac{{x\left( {\sqrt 3 + 1} \right)}}{2}\]
The boat has reached to the point \[B\] from the point \[A\] in \[20\] seconds and \[AB = x\]
\[\therefore \]Speed of the boat is \[v = \dfrac{x}{{20}}\]
\[\therefore \]The time taken by the boat from \[B\] to reach the base of the tower is \[t = \dfrac{y}{v}\]
Substitute \[y = \dfrac{{x\left( {\sqrt 3 + 1} \right)}}{2}\] and \[v = \dfrac{x}{{20}}\]
\[\therefore t = \dfrac{y}{v} = \dfrac{{\left\{ {\dfrac{{x\left( {\sqrt 3 + 1} \right)}}{2}} \right\}}}{{\left( {\dfrac{x}{{20}}} \right)}} = \dfrac{{x\left( {\sqrt 3 + 1} \right)}}{2} \times \dfrac{{20}}{x} = 10\left( {\sqrt 3 + 1} \right)\]

Hence option D is correct.

Note: To find the required time, we need to divide the distance traveled by the boat by the uniform speed of the boat. Therefore, first we calculate the speed of the boat and then the distance traveled by the boat has been calculated, which is further utilized to obtain the required time.