Question

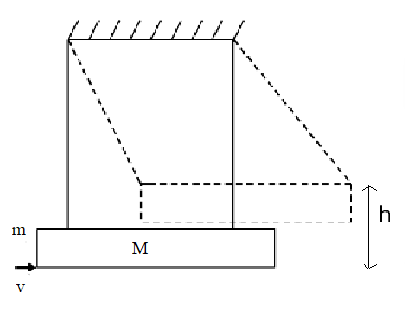
A large block of wood of mass M = 5.99 kg is hanging from two long massless cords. A bullet of mass m = 10 g is fired into the block and gets embedded in it. The (block + bullet) then swings upwards, their centre of mass rising a vertical distance h = 9.8 cm before the (block + bullet) pendulum comes momentarily to rest at the end of its arc. The speed of the bullet just before the collision is: (take g = $9.8\,m{s^{-2}}$)

A. 831.4 m/s
B. 841.4 m/s
C. 811.4 m/s
D. 821.4 m/s

Answer 1

Hint:To solve this question we use conservation of energy which means that energy before collision and energy after collision will be equal to the value of velocity after collision. By using velocity and applying conservation of momentum we get the required result.

Formula used:
Conservation of energy is given as:
\[(M + m)gh = \dfrac{1}{2}(M + m){v_1}^2\]
Where \[{v_1}\] is the velocity after collision, g is the acceleration due to gravity and h is the height.

Complete step by step solution:
According to energy conservation,
\[(M + m)gh = \dfrac{1}{2}(M + m){v_1}^2\]
After solving this, we get
\[{v_1} = \sqrt {2gh} \]
Also according to the conservation of momentum,
\[mv = (M + m){v_1}\]
\[\Rightarrow v = \left( {\dfrac{{M + m}}{m}} \right){v_1}\]
By solving this we get the result
\[\therefore v = 831.4\,m/s\]

Hence option A is the correct answer.

Note: Energy conservation is defined as the decision or practice of using less amount of energy. When we leave the room, we turn off all the lights or unplug appliances when they're not in use and we prefer walking instead of driving. All these are examples of energy conservation. In any closed system that is isolated from its surroundings then the total energy of that system is said to be conserved.