Question

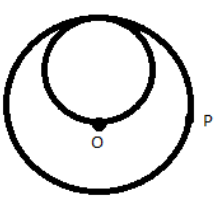
A lamina is made by removing a small disc of 2R diameter from a bigger disc of uniform mass density and radius 2R, as shown in figure. The moment of inertia of this lamina about the axis passing through O and P is ${I_o}$ and${I_p}$, respectively. Both these axes are perpendicular to the plane of the lamina. The ratio \[\dfrac{{{I_p}}}{{{I_o}}}\] to the nearest integer is:

A) $\dfrac{{13}}{{37}}$
B) $\dfrac{{37}}{{13}}$
C) $\dfrac{{73}}{{31}}$
D) $\dfrac{8}{{13}}$

Answer 1

Hint: First we found the moment of inertia about O and also found out the moment of inertia about P by subtracting the moment of inertia of cavity from the total part.

Complete step by step solution:

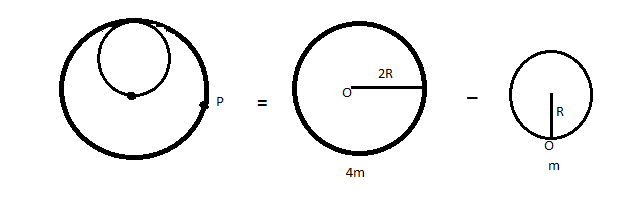
When we rotate this about O, then make a circle of radius 2R. Then first we find the moment of inertia of circle of radius 2Rand subtract moment of inertia of circle of radius R.
\[{I_0} = \dfrac{1}{2}\left( {4m} \right)\left( {2{R^2}} \right) - \left[ {\dfrac{1}{2}m{R^2} + m{R^2}} \right]\]
\[\Rightarrow 8m{R^2} - \dfrac{3}{2}m{R^2}\]
\[\Rightarrow \dfrac{{13}}{2}m{R^2}\]

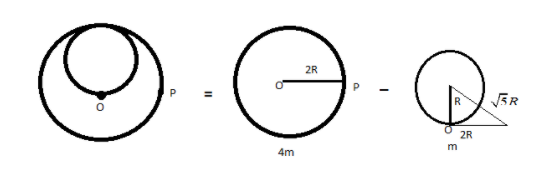
\[\Rightarrow {I_P} = \left[ {\dfrac{1}{2}\left( {4m} \right){{\left( {2R} \right)}^2} + 4m{{\left( {2R} \right)}^2}} \right] - \left[ {\dfrac{1}{2}m{R^2} + m{{\left( {\sqrt 5 R} \right)}^2}} \right]\]
\[\Rightarrow \left[ {\dfrac{1}{2} \times 4m \times 4{R^2} + 4m \times 4{R^2}} \right] - \left[ {\dfrac{1}{2}m{R^2} + 5m{R^2}} \right]\]
\[\Rightarrow \left[ {8m{R^2} + 16m{R^2}} \right] - \left[ {\dfrac{{11}}{2}m{R^2}} \right]\]
\[\Rightarrow 24m{R^2} - \dfrac{{11}}{2}m{R^2}\]
\[\Rightarrow m{R^2}\left[ {24 - \dfrac{{11}}{2}} \right]\]
\[\Rightarrow m{R^2}\left[ {\dfrac{{48 - 11}}{2}} \right]\]
\[\Rightarrow m{R^2}\left[ {\dfrac{{37}}{2}} \right]\]
\[ \Rightarrow \dfrac{{37}}{2}m{R^2}\]
Then the ratio of moment of inertia around P, to moment of inertia about O.
\[\Rightarrow \dfrac{{{I_p}}}{{{I_0}}} = \dfrac{{\dfrac{{37}}{2}}}{{\dfrac{{13}}{2}}} = \dfrac{{37}}{{13}}\]
\[\Rightarrow \boxed{\dfrac{{{I_p}}}{{{I_0}}} = \dfrac{{37}}{{13}}}\]

Note: When we find out the moment inertia around P, then we take a small sphere of radius R, but we should take the sphere radius of \[\sqrt 5 R\].