Question

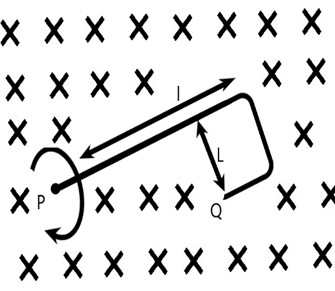
When a $'J'$ shaped conducting rod is rotating in its own plane with constant angular velocity $\omega $, about one of its ends $P$, in a uniform magnetic field $B$as shown then the magnitude of induced emf across it will be


A. $B\omega = \sqrt {{L^2} + {l^2}} $
B. $\dfrac{1}{2}B\omega {L^2}$
C. $\dfrac{1}{2}B\omega ({L^2} + {l^2})$
D. $\dfrac{1}{2}B\omega {l^2}$

Answer 1

Hint: When a bar magnet is moved into and out of the coil, an emf is produced in the coil. Motion in opposing directions results in emfs of the opposite signs, and reversing the poles will likewise reverse the emfs. The same outcomes are obtained by moving the coil rather than the magnet.

Complete step by step solution:
In the question, a $J$ shaped conducting rod is rotating in its plane with constant velocity $(\omega )$, the end point of the rod is $P$ in a uniform magnetic field $(B)$. Calculating the EMF of the two lengths of the conductor separately. Let displacement of $PQ$ be $x$, $\omega $ be the velocity and $dx$be small displacement along the length $l$ of the conductor, then the emf induced in the small element due to its motion is given by:
$De = B\omega xdx$

Integrate the aforementioned equation within the appropriate bounds to determine the net induced emf.
$\int\limits_0^e {De = \int\limits_0^l {B\omega xdx} }\\ $
$\Rightarrow e = B\omega [\dfrac{{{x^2}}}{2}]_0^l$
Apply the limit on the integrated equation, to determine emf induced between the centre of the rod and one of its side is, so the limit extends from:
$e = B\omega [\dfrac{{{l^2}}}{2}] - B\omega [\dfrac{{{0^2}}}{2}] \\$
$\Rightarrow e = B\omega [\dfrac{{{l^2}}}{2}]\,\,\,.....(i) \\$
The effective length of the circular path we took will be determined similarly. Since the falling object is a ring the projection of length of the ring along the length $L$ of the conductor,
$\int\limits_0^e {De = \int\limits_0^L {B\omega xdx} } \\ $
$\Rightarrow e = B\omega [\dfrac{{{x^2}}}{2}]_0^L$

Now apply the limit on the above integrated equation,
$e = B\omega [\dfrac{{{L^2}}}{2}] - B\omega [\dfrac{{{0^2}}}{2}] \\$
$\therefore e = B\omega [\dfrac{{{L^2}}}{2}]\,\,\,.....(ii) $
Add equation $(i)$ with $(ii)$ to find the total EMF, then:
$\therefore e = \dfrac{1}{2}B\omega ({l^2} + {L^2})$

Hence the correct option is C.

Note: The magnetic field's strength in the region encircled by the loop can then fluctuate over time. An induced EMF is produced whenever a coil's magnetic field or flux changes. No induced emf will exist if the magnetic flow is constant. If there was no change in the magnetic flux then there would have been no emf induced in the conductor.